ROZMAITOŚCI › Leksykon matematyczny

Wielościany toroidalne

Data ostatniej modyfikacji:
2013-12-9
Dział matematyki: 
geometria przestrzenna

Definicja:
Powierzchnia bez brzegu z genusem 1 (tzn. zawierająca jeden "otwór"), ograniczona wielokątami. Czasem dopuszcza się w definicji genus ≥ 1, zatem otworów może też być więcej.

 

Przykłady:

  • Sześcian z wydrążonym na przestrzał prostopadłościennym "kanałem".
  • Wielościenne "ramki".

     

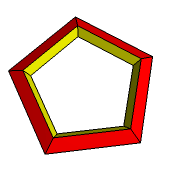
  • Istnieją wielościany toroidalne, których wszystkie ściany są wielokątami foremnymi. Mogą to być nawet tylko trójkąty równoboczne, np. w wielościanie Conway'a.

         

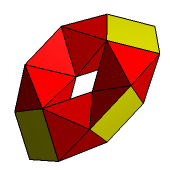
  • Wielościan Császára - ma wśród wielościanów toroidalnych najmniejszą możliwą liczbę wierzchołków - 7. Ponadto ma 14 trójkątnych ścian i 21 krawędzi (W-K+S=0). Nie ma przekątnych (wśród wielościanów wypukłych tę własność ma tylko czworościan, a jeśli istnieje jeszcze inny o tej własności, musi mieć genus co najmniej 6). Jest dualny do wielościanu Szilassiego.
    rysunek plik

  • Wielościan Szilassiego [czytaj: siloszsziego] - ma wśród wielościanów toroidalnych najmniejszą możliwą liczbę ścian - 7. Są one sześciokątami i każda z nich graniczy z każdą inną (wśród wielościanów wypukłych tę własność ma tylko czworościan). Ponadto ma 14 wierzchołków i 21 krawędzi (W-K+S=0). Jest dualny do wielościanu Császára.

  Kontrprzykłady:

  •  Żaden wielościan wypukły nie jest toroidalny bo jego genus wynosi 0.
  • Torus nie jest wielościanem toroidalnym, bo nie jest ograniczony wielokątami.

  • Toroidy (w szczególności torusy wielokątne) nie są wielościanami toroidalnymi, bo są to bryły obrotowe, czyli nie są ograniczone wielokątami. O torusach wielokątnych więcej można przeczytać na Portalu w dziale MAT-ŚWIAT w artykule Zakręcone graniastosłupy (1) i (2).
    animacja z mat-świata

 

Własności:

  • Wszystkie wielościany toroidalne o genusie 1 są topologicznie równoważne z torusem (jeśli genus wynosi n, to z n-torusem)
  • Charakterystyka Eulera χ wielościanów toroidalnych (czyli liczba 2-2g, gdzie g to genus powierzchni) wynosi 0 (jak dla torusa, gdyż jest to niezmiennik topologiczny). Jednocześnie jest to liczba, którą otrzymujemy ze wzoru wielościennego Eulera W-K+S (W - liczba wierzchołków, K-krawędzi, S - ścian).

 

Historia:

  • W 1949 roku wieku Węgier Ákos Császár podał przykład wielościanu toroidalnego o najmniejszej możliwej liczbie wierzchołków, wynoszącej 7. 
  • W 1977 roku węgierski matematyk Lajos Szilassi [wym. lojosz siloszszi] podał przykład wielościanu toroidalnego o najmniejszej możliwej liczbie ścian, wynoszącej 7. Jest on dualny do wielościanu Császára.
  • W 1997 roku angielski matematyk John Conway (twórca gry Life) podał przykład wielościanu toroidalnego z genusem 1 i wszystkich ścianach będących trójkątami równobocznymi. Jest ich 36. Do dziś nie jest znany przykład o mniejszej liczbie takich ścian.

 

Terminy pokrewne:

‹ Ww góręWstęga Möbiusa ›

Powrót na górę strony