Toroid

Toroid

Data ostatniej modyfikacji:
2009-02-17

Dział matematyki:

geometria przestrzenna

Pojęcia podstawowe

Definicja:
Powierzchnia obrotowa powstała przez obrót o kąt pełny dowolnej płaskiej krzywej zamkniętej wokół osi leżącej w płaszczyźnie tej krzywej, ale nieprzecinającej jej. W szczególności krzywa może mieć samoprzecięcia. Dopuszczalne jest też, by w trakcie obrotu wokół osi, figura wirowała dodatkowo w swojej płaszczyźnie wokół punktu wewnętrznego.

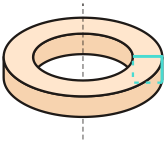
+ animacja z mat-świata

Przykłady:

Najprostszym przykładem toroidu jest torus pierścieniowy lub eliptyczny, otrzymane z obrotu odpowiednio okręgu lub elipsy.

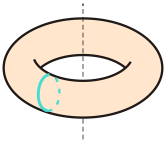
Toroidami są torusy wielokątne, czyli powierzchnie otrzymane z obrotu wielokąta wokół osi rozłącznej z nim, lecz leżącej w jego płaszczyźnie. Więcej o takich powierzchniach można przeczytać na Portalu w dziale MAT-ŚWIAT w artykule Zakręcone graniastosłupy (1) i (2).
animacja z mat-świata

Kontrprzykłady:

"Sześcian z dziurą" nie jest toroidem, bo nie jest powierzchnią obrotową.

Podobnie nie są toroidami inne wielościany toroidalne, czyli powierzchnie wielościenne z genusem 1 (tzn. zawierające jedną "dziurę").

Nie są toroidami powierzchnie zwane cytryną i jabłkiem, które powstają z obrotu łuku okręgu (odpowiednio mniejszego lub większego od półokręgu) wokół cięciwy łączącej końce tego łuku. Nie mają one pierścieniowego kształtu, bo nie powstają z obrotu wokół osi rozłącznej z obracaną figurą.
rysunek plik

Nie są toroidami torusy wrzecionowy i rogaty, bo nie mają pierściennego kształtu (oś ich obrotu nie jest rozłączna z obracanym okręgiem).
rysunek plik

Zastosowanie

W technice kształt toroidu nadaje się rdzeniom transformatorów przeznaczonych do zasilania urządzeń elektrycznych.