Tuzin dwunastościanów

O szczególnym znaczeniu liczby dwanaście w naszej kulturze nie trzeba chyba nikogo przekonywać. Rok liczy 12 miesięcy, jest 12 znaków zodiaku, doba podzielona jest na dwie części, z których każda liczy 12 godzin, Jezus powołał 12 apostołów, a w wizji św. Jana na głowie niewiasty obleczonej w słońce umieszczony był „wieniec z gwiazd dwunastu" (Ap 12,1). Liczbę tę wyróżniono również szczególna nazwą - tuzin.

Także w świecie wielościanów liczba 12 odgrywa znaczącą rolę. Istnieje sporo ważnych i interesujących wielościanów liczących właśnie tyle ścian. Poniżej prezentujemy tuzin dwunastościanów o przystających ścianach.

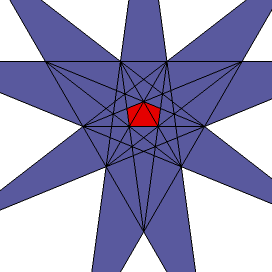
I. Czołowe miejsce należy się oczywiście dwunastościanowi foremnemu, będącemu jedną z pięciu brył platońskich (rys. 1). Jego stożkowanie prowadzi do trzech kolejnych wielościanów foremnych:

II. dwunastościanu gwiaździstego małego (rys. 2),
III. dwunastościanu wielkiego (rys. 3),
IV. dwunastościanu gwiaździstego wielkiego (rys. 4).
Wszystkie one należą do rodziny wielościanów Keplera-Poinsota.

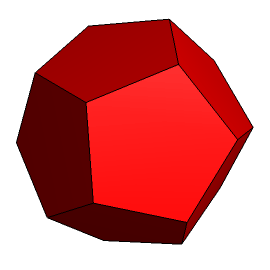
Rys. 1                                                                    Rys. 2   

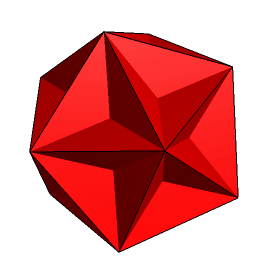
  Rys. 3                                                                   Rys. 4  

V. W wyniku stożkowania innego z wielościanów platońskich - dwudziestościanu można otrzymać dwunastościan, którego wszystkie ściany są przystającymi (ale nieforemnymi) pięciokątami. Może wydać się trochę dziwne, że w wyniku przedłużania ścian dwudziestościanu otrzymamy wielościan o innej liczbie ścian niż 20. Tajemnica polega na tym, że operację tę wykonujemy tylko w stosunku do odpowiednio wybranych ścian dwudziestościanu. W ten sposób 8 ścian wyjściowej bryły zostanie zakrytych. Rysunki 5 i 6 przedstawiają odpowiednio cały model oraz usytuowanie jego ściany na diagramie stożkowań dwudziestościanu.

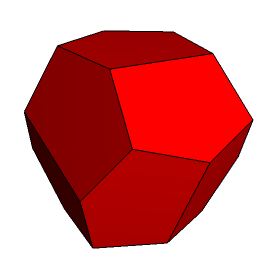
Rys. 5                                                                   Rys. 6

Wielościan ten jest interesujący również dlatego, że w podobny mu sposób krystalizuje minerał żelaza - piryt (fot. 1). Być może właśnie obserwacja kryształów tego minerału doprowadziła starożytnych Greków do odkrycia dwunastościanu foremnego.

 Fot. 1

Wykonanie modelu tego wielościanu jest proste. Kliknięcie w poniższy link otwiera w nowym oknie jego siatkę.

dwunastościan nieforemny

VI. Kolejnym dwunastościanem na naszej liście jest jeden z wielościanów Catalana - dwunastościan rombowy (rys. 7). Ten odkryty przez Keplera wielościan jest ze wszech miar godny uwagi, a jego niebywałym własnościom można poświęcić więcej niż jeden artykuł. Polecam szczególnie książkę Jana Baranowskiego „Dwunastościan rombowy" (WSiP, Warszawa 1988).

 Rys. 7

W tym miejscu wspomnijmy, że dwunastościanami rombowymi można wypełnić przestrzeń (rys. 8) oraz że wielościan ten występuje w przyrodzie w postaci kryształów granatu (fot. 2).

 Rys. 8

 Fot. 2

VII. Pierwsze stożkowanie dwunastościanu rombowego jest również bardzo atrakcyjnym dwunastościanem (rys. 9, 10).

Rys. 9                                                                  Rys. 10    

Jak widać wielościan ten powstaje w wyniku doklejenia do każdej ściany dwunastościanu rombowego odpowiedniej piramidy. Zachęcamy wszystkich do samodzielnego wykonania modelu tego wielościanu w oparciu o zamieszczone wyżej rysunki. Dwunastościan ten, podobnie jak poprzedni, również parkietuje przestrzeń (rys. 11).

 Rys. 11

VIII. Mniej więcej pół wieku temu chorwacki matematyk Stanko Bilinski opisał inny dwunastościan rombowy (rys. 12).

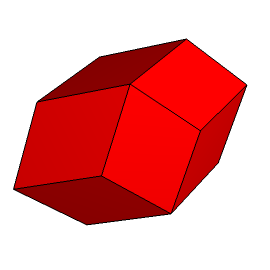
Rys. 12

Jego ściany są rombami o stosunku przekątnych będącym „złotą liczbą" - ½(1+√5). Stosunek długości przekątnych ścian dwunastościanu rombowego Keplera wynosił √2. Kliknięcie w link poniżej otwiera w nowym oknie jego siatkę.

dwunastościan rombowy Bilinskiego

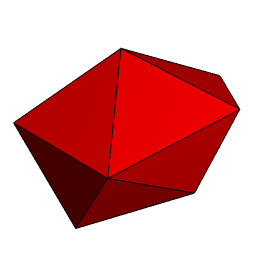
IX. Wielościan o dwunastu foremnych ścianach można znaleźć również wśród wielościanów Johnsona. Jest nim dwuklinoid przycięty (J 84), a jego ścianami są trójkąty równoboczne (rys. 13).

X-XI. Kolejne dwa dwunastościany na naszej liście to wielościany dualne do graniastosłupa i antygraniastosłupa sześciokątnego. Pierwszy z nich do dwupiramida sześciokątna (rys. 14), a drugi to dwunastościan deltoidowy (rys. 15).

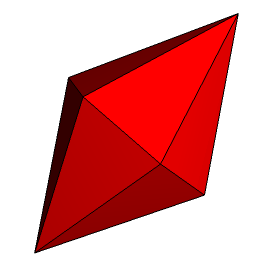
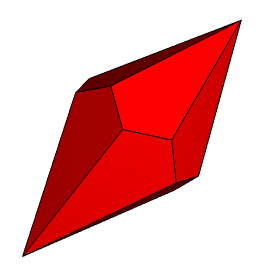
Rys. 14                                                                 Rys. 15 

Więcej na temat konstrukcji ściany wielościanu dualnego do danego można przeczytać tutaj. Kliknięcie w odpowiedni link otwiera w nowym oknie siatkę wielościanu.

dwupiramida sześciokątna                         dwunastościan deltoidowy

XII. Ostatni z prezentowanych dwunastościanów (rys. 16) można określić mianem podstawki na dwunastościan foremny. Wystarczy tylko spojrzeć na rys. 17.

Rys. 16                                                             Rys. 17   

Ściana tego wielościanu jest fragmentem pięciokąta foremnego (rys. 18), a jego wierzchołki są wierzchołkami sześcianu (rys. 19).

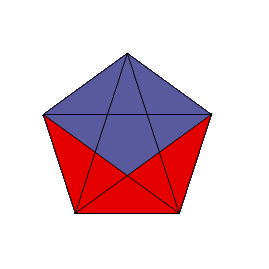
Rys. 18                                                           Rys. 19        

Wykonanie modelu ostatniego z prezentowanych dwunastościanów nie jest zadaniem specjalnie trudnym, ale dobre sklejenie wierzchołków wymaga pewnej staranności. Kliknięcie w link poniżej otwiera w nowym oknie element siatki złożony z dwóch ścian bryły.

podstawka na dwunastościan foremny, element siatki

Do wykonania całego modelu potrzeba oczywiście sześciu takich elementów.

Wizerunki wielościanów zostały wyeksportowane z programu Great Stella. Siatki zostały przygotowane za pomocą programu Wingeom.