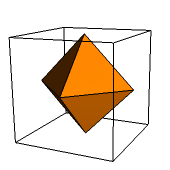
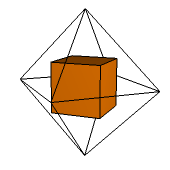
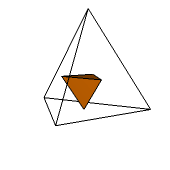
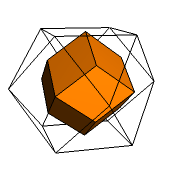
Środki ścian sześcianu wyznaczają ośmiościan foremny (ryc. 1). Jest też na odwrót - środki ścian ośmiościanu foremnego wyznaczają sześcian (ryc. 2). Dlatego mówimy o tych wielościanach, że są dualne (krawędzią łączymy te wierzchołki, które leżą na środkach ścian sąsiednich).
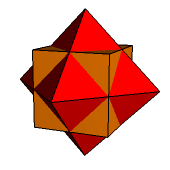
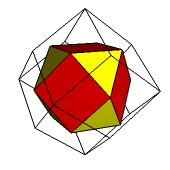
Zauważmy, że po odpowiednim dobraniu długości krawędzi wielościanów dualnych możemy tworzyć nowe, ciekawe bryły, będące kompozycjami (czyli przenikającymi się nawzajem nałożeniami) wielościanów dualnych (ryc. 3).
|
Ryc. 1 |
Ryc. 2 |
Ryc. 3 |
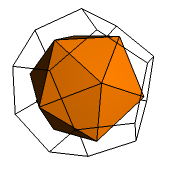
Parę wielościanów dualnych tworzą też foremne dwunastościan i dwudziestościan (ryc. 4-5). Na ryc. 6 pokazano ich kompozycję.
|
Ryc. 4 |
Ryc. 5 |
Ryc. 6 |
Natomiast wielościanem dualnym do czworościanu jest on sam (ryc. 7). W kompozycji ze sobą daje gwiazdę ośmioramienną nazywaną stella octangula (ryc. 8).
|
Ryc. 7 |
Ryc. 8 |
Wielościany dualne mają tyle samo krawędzi, a liczba ścian jednego z nich jest taka, jak liczba wierzchołków drugiego (co wynika z definicji dualności).
Podobnie jak wielościany platońskie również wielościany Keplera-Poinsota (foremne, niewypukłe) można połączyć w dualne pary. Jako dobre ćwiczenie wyobraźni proponuję samodzielne znalezienie tych par.
Bryły foremne (wypukłe i niewypukłe) nie dają jako dualnych żadnych nowych obiektów. Nowe wielościany, nie omawiane wcześniej w Galerii, powstają natomiast jako dualne do archimedesowych. Proces ten jest bardziej skomplikowany niż w przypadku brył platońskich i nie polega on na łączeniu środków odpowiednich ścian wielościanów. Ryc. 9-10 przedstawiają wielościan dualny do archimedesowego sześcio-ośmiościanu. Jest nim 12-ścian rombowy, a oba razem tworzą ciekawą kompozycję (ryc. 11).
|
Ryc. 9 |
Ryc. 10 |
Ryc. 11 |
W 1865 roku matematyk belgijski Eugene Catalan opisał wielościany dualne do wszystkich wielościanów archimedesowych. Ściany tych wielościanów nie są już wielokątami foremnymi, ale ponieważ wielościany archimedesowe mają identyczne wierzchołki, zatem wszystkie ściany w danym wielościanie Catalana są jednakowe. Natomiast naroża nie są przystające, bo w danym wielościanie archimedesowym nie wszystkie ściany są przystające.
Więcej na temat konstrukcji ścian wielościanów Catalana można przeczytać na stronie Siatki wielościanów Catalana. Zachęcam też do samodzielnego dopasowania pozostałych wielościanów archimedesowych do dualnych do nich wielościanów Catalana.
Rysunki wielościanów prezentowane wyżej zostały wyeksportowane z programu Great Stella.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
Dualność
Dualność to doklejanie ostrosłupów na inne wielościany.(-:
To nie tak
Jak się patrzy na modele niektórych wielościanów Catalana, to można odnieść takie wrażenie. Z tym, że nie jest obojętna wysokość doklejanych ostrosłupów. Jednakże rzut oka na inne wielościany z tej grupy wystarcza do stwierdzenia, że nie jest to prawdą. Formalna definicja dualności jest dość skomplikowana i nie da się tego procesu tak zredukować.