Zbadajmy możliwe stożkowania najprostszych i najbardziej regularnych brył - wielościanów platońskich. Wielościanów tych jest pięć, ale w zależności od stopnia skomplikowania swojej budowy, mogą mieć 0, kilka lub nawet kilkadziesiąt możliwych stożkowań.
Czworościan foremny i sześcian nie mają żadnych stożkowań. Przedłużanie ich ścian nie daje nowych przecięć.
Przyjrzyjmy się teraz ośmiościanowi foremnemu (rys. 1). Trzy ściany otaczające daną ścianę po przedłużeniu utworzą nad nią czworościan foremny (rys. 2).
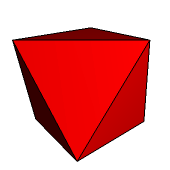
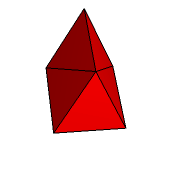
Rys. 1 Rys. 2
Zastosowanie tego procesu do wszystkich ścian prowadzi do formy gwiaździstej ośmiościanu (rys. 3). Jest to stella octangula - znana kompozycja dwóch czworościanów foremnych (rys. 4). Po raz pierwszy opisał ją Luca Pacioli w swoim dziele De divina proportione w roku 1509. Figuruje tam ona pod nazwą octaedron elvatus, co można przetłumaczyć jako "powiększony ośmiościan". Jest to jedyna gwiaździsta forma ośmiościanu foremnego.
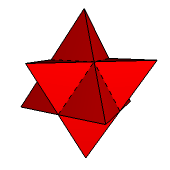
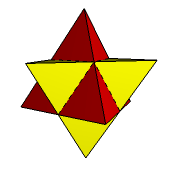
Rys. 3 Rys. 4
Opisanie stożkowań foremnego dwunastościanu (rys. 5) również nie jest zadaniem zbyt trudnym. Pierwszy krok to zbudowanie piramid nad każdą ścianą tego wielościanu (rys. 6). W wyniku tego powstanie wielościan, którego ściany są pentagramami (rys. 7), będący jednym z wielościanów Keplera-Poinsota (to dwunastościan gwiaździsty mały).
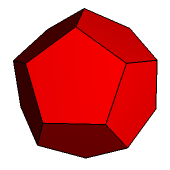
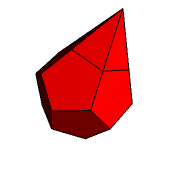

Rys. 5 Rys. 6 Rys. 7
Uzupełnienie pentagramów do pięciokątów foremnych prowadzi do kolejnego stożkowania dwunastościanu. Otrzymujemy kolejny wielościan Keplera-Poinsota - dwunastościan wielki (rys. 8). W ostatnim kroku możemy przedłużyć trzy ściany otaczające każde z trójściennych zagłębień (rys. 9). W wyniku tego otrzymamy ostatnią gwiaździstą formę dwunastościanu (rys. 10). Również i ten wielościan jest jednym z wielościanów Keplera-Poinsota (to dwunastościan gwiaździsty wielki).
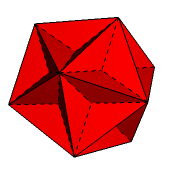
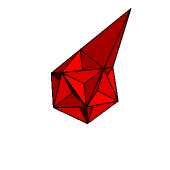

Rys. 8 Rys. 9 Rys. 10
Do przedstawiania stożkowań używa się specjalnego diagramu, pokazującego efekt kolejnego przedłużania krawędzi zadanej ściany wyjściowego wielościanu. Diagram ten dla dwunastościanu foremnego wygląda tak, jak na rys. 11. Liczba 0 oznacza ścianę bryły wyjściowej, 1 to ściana dwunastościanu gwiaździstego małego, 2 - dwunastościanu wielkiego i wreszcie 3 - dwunastościanu gwiaździstego wielkiego.
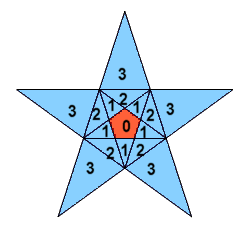
Rys. 11
Pozostał problem stożkowania ostatniego z wielościanów platońskich - dwudziestościanu foremnego (rys. 12). Pierwszy krok można wykonać stosunkowo łatwo. Podobnie jak wcześniej nad każdą ze ścian powstanie ostrosłup. Kąt dwuścienny między ścianami dwudziestościanu ma stosunkowo dużą miarę (około 138,19°), więc ostrosłupy te będą dość płaskie. Ich ściany będą nachylone do podstawy pod kątem około 41,81° (dlaczego?). Cały wielościan gwiaździsty będzie składał się z 20 nieforemnych sześciokątów (rys. 13, 14).
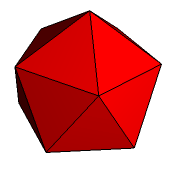


Rys. 12 Rys. 13 Rys. 14
Przedłużenie tych ścian w odpowiedni sposób daje kolejną stellację dwudziestościanu (rys. 15). Tym razem ściany są układami dwóch trójkątów równobocznych (rys. 16), a cała bryła jest kompozycją 5 ośmiościanów foremnych (rys. 17).


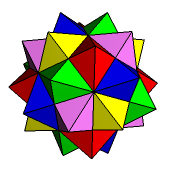
Rys. 15 Rys. 16 Rys. 17
Do końca XIX wieku skonstruowano kilkanaście stożkowań dwudziestościanu. Wykazano, że jest wśród nich także czwarty z wielościanów Keplera-Poinsota - dwudziestościan wielki (rys. 18) oraz foremne kompozycje 5 i 10 czworościanów (rys. 19, 20). Jednakże problem pełnego opisu form gwiaździstych dwudziestościanu pozostawał otwarty.



Rys. 18 Rys. 19 Rys. 20
Wynikało to z faktu, że diagram stellacyjny dwudziestościanu jest dość skomplikowany (rys. 21). Do ponumerowania jego komórek potrzebne są liczby od 0 do 13, a różne kombinacje tych komórek (choć nie wszystkie możliwe) dają różne stożkowania dwudziestościanu foremnego.
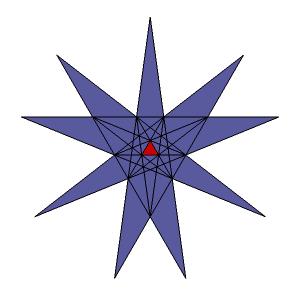
Rys. 21
Dopiero w roku 1938 Harold Scott MacDonald Coxeter z Patrickiem Du Val oraz dwoma innymi matematykami H.T. Flatherem (który wykonał modele kartonowe) i Johnem Flindersem Petrie (który wykonał rysunki brył) opublikowali pracę Fifty nine icosahedra (59 dwudziestościanów). Przyjmując pewne dość naturalne założenia odnośnie sposobu tworzenia form gwiaździstych, opracowane wcześniej przez Jeffreya Charlesa Percy'ego Millera, wykazali, że istnieje 58 możliwych stożkowań dwudziestościanu (wyjściowy dwudziestościan foremny plus 58 jego stożkowań dają tytułowe 59 dwudziestościanów). Opisy wszystkich tych stożkowań można znaleźć tutaj.
W 2002 roku Guy Inchbald kwestionując konieczność wszystkich poczynionych przez Millera założeń, wskazał kilka innych przykładów stożkowań dwudziestościanu. Jego pracę zatytułowaną "In search of the lost icosahedra" (W poszukiwaniu zagubionych dwudziestościanów) można znaleźć tutaj.
W przypadku bardziej skomplikowanych wielościanów liczba ich stożkowań jest olbrzymia. Rozwój komputerów pozwolił na stworzenie algorytmów obliczania ilości stożkowań dowolnego wielościanu. Na przykład liczba stożkowań archimedesowego dwudziesto-dwunastościanu rombowego wielkiego (rys. 22) przekracza 10 miliardów. Na rys. 23 pokazano ostatnią możliwą stellację tego wielościanu.
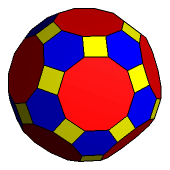

Rys. 22 Rys. 23
Na zakończenie zachęcamy do ustalenia, jak wyglądają pierwsze stożkowania dwóch innych wielościanów archimedesowych: sześcio-ośmiościanu (rys. 24) oraz dwudziesto-dwunastościanu (rys. 25).
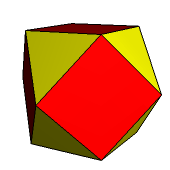

Rys. 24 Rys. 25
Rysunki wielościanów prezentowane na tej stronie zostały wyeksportowane z programu Great Stella.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Odpowiedź
Pierwszym stożkowaniem sześcio-ośmiościanu będzie kompozycja sześcianu z ośmiościanem, a dwudziesto-dwunastościanu - kompozycja dwudziestościanu i dwunastościanu.
Zgadza się
Zgadza się, tak właśnie jest.