Pod pojęciem stożkowania (ang. stellation, w języku polskim używa się też czasem określenia "rozgwieżdżanie" lub "stellacja") należy rozumieć proces przedłużania ścian danego wielościanu aż do ich ponownego przecięcia. Proces ten jest na tyle skomplikowany, że nie doczekał się jak dotąd ścisłej definicji i matematycy zajmujący się tą tematyką mówiąc o stożkowaniu nie zawsze myślą o tym samym. W wyniku stożkowania na bazie wyjściowego wielościanu powstają nowe wielościany, których ściany przecinając się, tworzą gwiaździstą strukturę. Pod pojęciem stożkowania można rozumieć również wielościan powstały w wyniku wspomnianego procesu. Na każdy niewypukły wielościan można spojrzeć jako na efekt przedłużania ścian pewnego wielościanu wypukłego. Wobec tego stożkowanie jest dobrą odpowiedzią na pytanie skąd się biorą bryłki.
W przypadkach najprostszych wielościanów można samodzielnie przekonać się jak wyglądają ich stożkowania. Ostrosłupy trójkątne i czworokątne nie tworzą form gwiaździstych. Podobnie nie ma ich żaden prostopadłościan (dlaczego?).
Popatrzmy na ostrosłup prawidłowy pięciokątny (rys. 1). Przedłużenie krawędzi jego podstawy prowadzi do powstania pentagramu (rys. 2) i dlatego w wyniku stożkowania powstanie ostrosłup o podstawie będącej pentagramem i przecinających się ścianach bocznych (rys. 3-5).
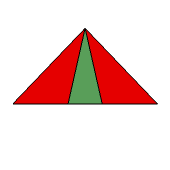
Rys. 1 Rys. 2 Rys. 3
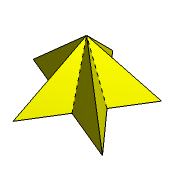
Rys. 4 Rys. 5
Podobnie rzecz się ma z prawidłowym graniastosłupem pięciokątnym (rys. 6-8).
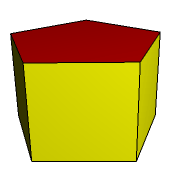
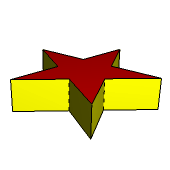
Rys. 6 Rys. 7 Rys. 8
W wyniku przedłużania krawędzi sześciokąta foremnego powstaje "gwiazda Dawida" (rys. 9), która z matematycznego punktu widzenia nie jest wielokątem gwiaździstym tylko układem dwóch przenikających się wzajemnie trójkątów równobocznych. Dlatego w wyniku stożkowania prawidłowego graniastosłupa sześciokątnego powstanie kompozycja dwóch graniastosłupów trójkątnych (rys. 9-11). A jak wygląda forma gwiaździsta prawidłowego ostrosłupa sześciokątnego?
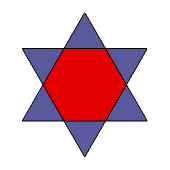
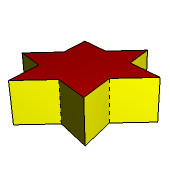
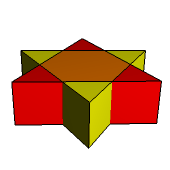
Rys. 9 Rys. 10 Rys. 11
Wizerunki wielościanów prezentowane na tej stronie zostały wyeksportowane z programu Great Stella.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
