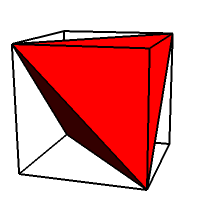
Pierwszą opisaną kompozycją wielościanów był układ dwóch wzajemnie przenikających się czworościanów foremnych (ryc. 1). Od czasów Keplera nosi on nazwę stella octangula (gwiazda ośmioramienna). Jednak bryła ta znana była już wcześniej. Po raz pierwszy opisał ją w 1509 roku w swoim dziele De divina proportione (boska proporcja) Luca Pacioli, a jej pierwszy "portret" wyszedł spod ręki Leonarda da Vinci. Wtedy nazywano ją octaedron elevatus (ośmiościan dobudowany), gdyż można ją otrzymać także w wyniku doklejenia czworościanu foremnego do każdej ściany ośmiościanu foremnego.
|
Ryc. 1 |
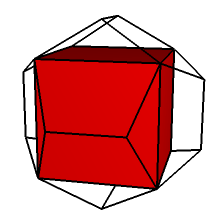
Ryc. 2 |
Ryc. 3 |
Również w XVI wieku pojawiły się kompozycje pozostałych dualnych par platońskich:
- sześcian + ośmiościan (ryc. 2),
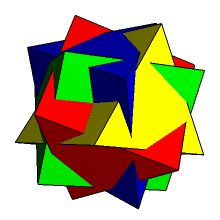
- dwunastościan + dwudziestościan (ryc. 3).
Na stellę octangulę można spojrzeć jako na dwa czworościany foremne mieszczące się w sześcianie (ryc. 4). W analogiczny sposób (tzn. wybierając odpowiednie wierzchołki) można umieścić sześcian w dwunastościanie foremnym (ryc. 5).
|
Ryc. 4 |
Ryc. 5 |
Można to uczynić na 5 sposobów, a te 5 brył wzięte na raz daje piękną kompozycję pięciu sześcianów (ryc. 6). Zastępując każdy sześcian w tej kompozycji dualnym do niego ośmiościanem (położonym względem sześcianu jak na ryc. 2) otrzymujemy kompozycję pięciu ośmiościanów (ryc. 7).
|
Ryc. 6 |
Ryc. 7 |
Kolejne interesujące kompozycje otrzymamy zastępując sześciany czworościanami. Jeżeli w miejsce każdego z pięciu sześcianów wstawimy jeden czworościan (zgodnie z ryc. 4) otrzymamy kompozycję pięciu czworościanów (ryc. 8). Zastępując każdy sześcian stellą octangulą otrzymamy kompozycję dziesięciu czworościanów (ryc. 9). Opis wykonania modelu kompozycji pięciu czworościanów w wersji ściankowej i ażurowej znajduje się tutaj.
|
Ryc. 8 |
Ryc. 9 |
Ściany każdego z czworościanów z tej ostatniej kompozycji leżą w płaszczyznach ścian innych czworościanów, dlatego też trudno jest pokolorować je w ten sposób, by poszczególne składniki kompozycji były wyraźnie widoczne.
Kompozycje z ryc. 6-9 zostały po raz pierwszy opisane w roku 1876 przez niemieckiego matematyka Edmunda Hessa. Wraz ze stellą octangulą można traktować je jako odpowiedniki wielościanów platońskich wśród kompozycji. Wszystkie ich ściany, wierzchołki oraz krawędzie są identyczne. Dlatego też uważa się je za kompozycje foremne. Okazuje się, że ani dwunastościany, ani dwudziestościany, ani żadne z wielościanów Keplera-Poinsota nie tworzą tak regularnych kompozycji, zatem istnieje dokładnie pięć foremnych kompozycji.
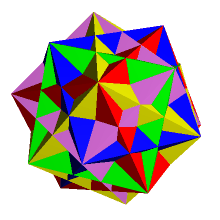
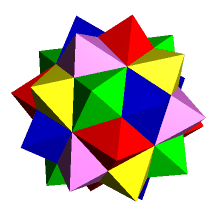
Dokładnie sto lat później - w roku 1976 - John Skilling opisał wszystkie jednorodne kompozycje wielościanów jednorodnych. Składnikami tych kompozycji są wielościany jednorodne, które tak położone są względem siebie, że wszystkie wierzchołki w kompozycji są przystające. Istnieje 75 takich układów. Niektóre z nich są stosunkowo proste (ryc. 10), ale jest też i taka, w której liczba widocznych na zewnątrz ścianek przekracza 3500 (ryc. 11). Interesujący jest fakt, że ścianami każdej z tych dwóch kompozycji są tylko trójkąty równoboczne i kwadraty.
|
Ryc. 10 |
Ryc. 11 |
Zachęcam wszystkich do przyjrzenia się prezentowanym dalej zdjęciom i samodzielnego ustalenia, które z prezentowanych na nich kompozycji wielościanów są kompozycjami jednorodnymi.
Wizerunki wielościanów prezentowane powyżej oraz siatki większości modeli prezentowanych w tej części galerii zostały wyeksportowane z programu Geat Stella.









 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
