Pięć czworościanów

Kompozycja pięciu czworościanów foremnych mieszczących się wewnątrz dwunastościanu foremnego jest jedną z najbardziej atrakcyjnych kompozycji wielościennych. Jej struktura jest na tyle prosta, że poszczególne czworościany są doskonale widoczne, ale z drugiej strony tworzą one bardzo intrygujący układ, który prowokuje i zachęca do uważniejszego przyjrzenia się. Kompozycja istnieje w dwóch enancjomorficznych (tzn. związanych z orientacją) wersjach (rys. 1-2), które mają się do siebie nawzajem jak lewa dłoń do prawej.

Rys. 1                                                                  Rys. 2  

Kompozycja pięciu czworościanów jest jednym ze stożkowań dwudziestościanu i wykorzystując diagram stellacyjny tego ostatniego (rys. 3) można przygotować element siatki pozwalający wykonać model.

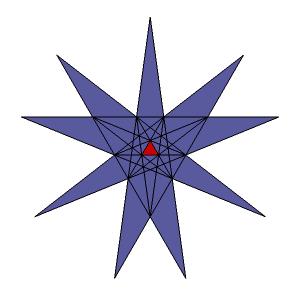
Rys. 3

Na rys. 4 i 5 zaznaczone są odpowiednie obszary na diagramie dla obu wersji kompozycji.

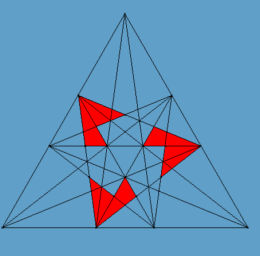
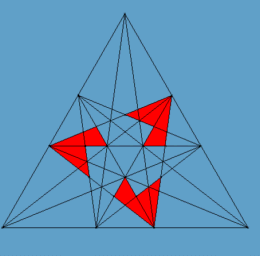
 Rys. 4                                                                Rys. 5      

Wykonanie modelu kompozycji pięciu czworościanów wymaga dużej staranności. Liczba potrzebnych elementów jest wprawdzie stosunkowo niewielka, ale ich łączenie (zwłaszcza pod koniec pracy) może sprawić kłopot. Kliknięcie w link poniżej otwiera w nowym oknie odpowiedni diagram.

pięć czworościanów element siatki

Do wykonania całego modelu potrzeba 20 elementów (po 4 w każdym z pięciu kolorów). Linie przerywane oznaczają krawędzie wklęsłe (zagięcia „do góry"). Niektóre skrzydełka na diagramie są zbędne - w miarę doklejania kolejnych części należy samodzielnie zdecydować, które w danym momencie się przydadzą, a które można odciąć. Ostatnie dwa elementy najlepiej pociąć na pojedyncze ścianki i przyklejać każdą z nich osobno.

Pięć czworościanów wyróżnia się wśród innych kompozycji również tym, że krawędzie jej poszczególnych składników nie przecinają się wzajemnie. Daje to możliwość zbudowania bardzo atrakcyjnego ażurowego modelu tej kompozycji (fot. 1).

Fot. 1 

Model ten pozwala niejako zajrzeć do środka i jeszcze lepiej zgłębić strukturę całego układu. Kluczem do jego zbudowania jest właściwe dobranie „grubości" krawędzi czworościanów. Jeżeli będzie ona zbyt mała, model nie będzie się sztywno trzymał (czworościany będą miały swobodę ruchu), a jeżeli będzie zbyt duża, to czworościany nie zmieszczą się jeden w drugim.

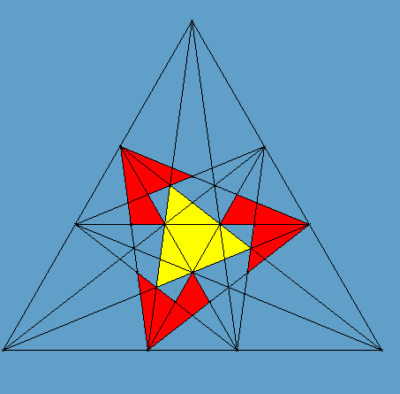
Rys. 6

 Rysunek 6 pokazuje wzajemną relację między dwoma składnikami kompozycji - żółty trójkąt to ślad, jaki zostawia jeden czworościan przebijając ścianę drugiego. Analiza tego rysunku i trochę (nieco żmudnych) rachunków pozwalają ustalić, że stosunek długości krawędzi do jej „grubości" powinien wynosić ok. 12,089675. Dla potrzeb wykonania modelu w zupełności wystarczy przyjąć, że stosunek ten jest równy 12. Każdy czworościan zbudowany jest z 6 „belek" reprezentujących jego krawędzie. Skonstruowanie pojedynczej „belki" jest dobrym (choć nie całkiem prostym) ćwiczeniem ze stereometrii. Kliknięcie w link poniżej otwiera w nowym oknie odpowiednią siatkę.

 pięć czworościanów, model ażurowy - element siatki

Do wykonania całego modelu potrzeba 30 elementów (po 6 w każdym z pięciu kolorów). Wykonanie pojedynczego elementu nie jest bardzo trudne (choć jak zawsze wymaga pewnej staranności). Najlepiej zacząć od dokładnego sklejenia najdłuższej krawędzi. Ścianki bez skrzydełek należy przykleić jako ostatnie. Sklejenie czworościanu z 6 „belek" jest już proste, jednak połączenie wszystkich 30 w całość stanowi nie lada wyzwanie. Podstawą sukcesu jest właściwe umieszczenie drugiego czworościanu względem pierwszego. Seria zdjęć zamieszczona poniżej powinna ułatwić wykonanie modelu. Kliknięcie w miniaturę otwiera w nowym oknie duże zdjęcie.

Rysunki 1-3 zostały wyeksportowane z programu Great Stella, pozostałe rysunki oraz siatki zostały przygotowane w programie Wingeom.