Stella octangula z wariacjami

Najprostszy z wielościanów platońskich - czworościan foremny - tworzy bardzo interesujące kompozycje. Pisaliśmy już o nich w Galerii tutaj. Najprostszą i jednocześnie najważniejszą z nich jest stella octangula, czyli gwiazda ośmioramienna (rys. 1).

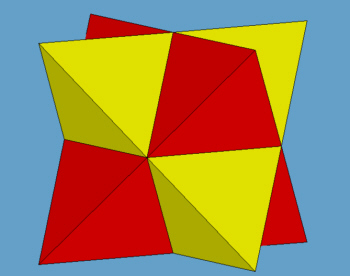
rys. 1

Jak łatwo widać jest to kompozycja dwóch czworościanów foremnych. Wykonanie jej modelu nie powinno sprawić nikomu problemu. Wystarczy przygotowac 8 małych czworościanów (po 4 w dwóch kolorach) i odpowiednio je połączyć za pomocą podwójnych skrzydełek. Można też dokleić je do ścian przygotowanego wcześniej ośmiościanu foremnego. Kliknięcie w poniższe linki otwiera w nowych oknach odpowiednie siatki.

czworościan                                  ośmiościan

Spójrzmy teraz na stellę octangulę z innej perspektywy. Poprowadźmy prostą przez środki dwóch przeciwległych krawędzi czworościanu (rys. 2).

rys. 2 

Jeżeli obrócimy czworościan wokół tej prostej o kąt 180º, to przejdzie sam na siebie. Jeżeli natomiast obrócimy go o 90°, to czworościan i jego obraz utworzą właśnie stellę octangulę. Wyjściowy czworościan możemy oczywiście obracać o dowolny inny kąt. W wyniku obrotu o wielokrotności kąta 60° otrzymamy kompozycję trzech czworościanów (rys. 3).

rys. 3 

Obroty o wielokrotności 45° dają 4 czworościany (rys. 4). Ta ostatnia kompozycja jest w istocie układem dwóch stelli octanguli.

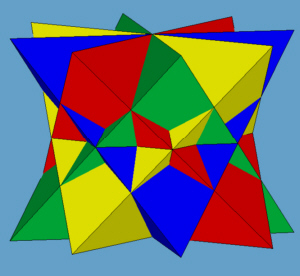
rys. 4 

Ustalając odpowiednio kąty obrotu, możemy uzyskać kompozycję dowolnej liczby czworościanów (np. ośmiu - rys. 5).

rys. 5 

Wyznaczenie elementów siatek tych kompozycji nie jest tak proste jak w przypadku stelli, ale nie wymaga specjalnej wiedzy matematycznej. Wystarczy uważne przyjrzenie się rysunkom. Posłużmy się przykładem kompozycji trzech czworościanów. Przyjmijmy oznaczenia jak na rys. 6.

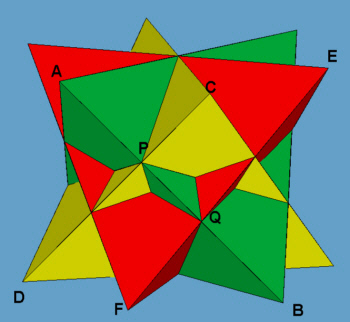
rys. 6 

Kluczem do wyznaczenia elementów siatki tej kompozycji jest znalezienie stosunku długości odcinków, na jakie krawędź jednego czworościanu dzieli krawędź drugiego (czyli np. AP/PB). Krawędzie AB oraz CD przecinają się, zatem punkty A, B, C i D leżą na jednej płaszczyźnie. Co więcej - punkty A i C leżą oczywiście na płaszczyźnie wyznaczonej przez wszystkie „górne" wierzchołki kompozycji, a punkty B i D na płaszczyźnie wyznaczonej przez „dolne". Płaszczyzny te są oczywiście równoległe. Oznacza to, że odcinki AC oraz BD są również równoległe, a czworokąt ACBD jest trapezem. Punkt P jest punktem przecięcia przekątnych tego trapezu. Wobec tego trójkąty DBP oraz CAP są podobne. Wobec tego AP/PB=AC/DB. Spójrzmy teraz na płaszczyzny wyznaczone przez „górne" i „dolne" wierzchołki kompozycji (rys. 7).

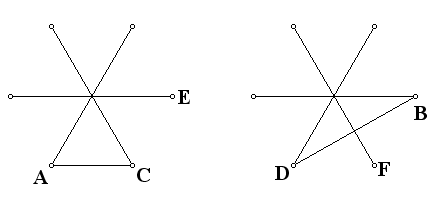
rys. 7

Jeżeli krawędzie czworościanów mają długość a, to AC=a/2 oraz BD= a√3/2 (dlaczego?). Zatem AP/PB = 1√3=√3/3. Stąd po krótkich przekształceniach mamy AP/AB = (√3-1)/2 ≈ 0,366. Przez symetrię widać, że zachodzi AP=BQ oraz że w identyczny sposób podzielone są wszystkie „boczne" krawędzie rozważanej kompozycji. Poprowadźmy odpowiednie linie łączące punkty na krawędziach jednej ściany (rys. 8).

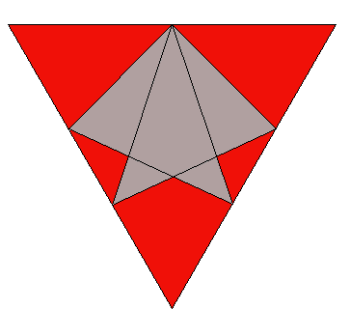
rys. 8 

Fragmenty ścian widoczne na zewnątrz kompozycji oznaczone są kolorem czerwonym. Do wykonania modelu kompozycji należy przygotować trzy rodzaje elementów - A, B oraz C. Element C jest lustrzanym odbiciem elementu B. Potrzeba 12 elementów typu A (po 4 w każdym z trzech kolorów) oraz po 6 elementów typu B i C (po 2 w każdym z trzech kolorów). Kształt elementów pozwala na ich natychmiastową lokalizację na modelu. Kliknięcie w poniższe linki otwiera w nowych oknach odpowiednie siatki. Linie przerywane oznaczają krawędzie wklęsłe (zagięcia do góry).

element A                                   elementy B i C

W analogiczny sposób można wyznaczyć elementy siatki do wykonania kompozycji 4 czworościanów. Wykonanie odpowiednich obliczeń oraz przygotowanie elementów siatki pozostawiamy zainteresowanym jako zadanie do samodzielnego rozwiazania.

Rysunki i siatki zostały przygotowane za pomocą programu Wingeom.