Matematyka pod stopami (2)

W artykule Matematyczne mozaiki w sercu Wenecji możemy podziwiać wspaniałe mozaiki z bazyliki św. Marka, jednak wcale nie trzeba wybierać się w tak daleką podróż, by zobaczyć interesujące z matematycznego punktu widzenia posadzki, chodniki, czy wycieraczki. Wystarczy zwrócić uwagę na to, po czym chodzimy na co dzień.

Kostki brukowe mają zazwyczaj kształt figur, którymi można szczelnie wypełnić płaszczyznę (powstaje wtedy parkietaż). Nawet jeżeli są to zwyczajne prostokąty, to mogą być układane na kilka różnych sposobów. Można też napotkać kostki o bardziej oryginalnych kształtach.

Niektóre parkietaże powstają z kostek jednego kształtu, inne z dwóch, trzech lub więcej. Jeśli do parkietażu wykorzystujemy tylko jeden rodzaj kostek w kształcie wielokąta foremnego, parkietaż nazywamy (w analogii do wielościanu) platońskim lub foremnym. Ile jest takich możliwych parkietaży? Jeśli używamy kostek w kształcie różnych wielokątów foremnych, przy czym wszystkie węzły parkietażu są identyczne, parkietaż nazywamy (znowu w analogii do wielościanu) archimedesowym lub półforemnym. Czy potrafisz wskazać ich przykłady na poniższych zdjęciach?

A gdzie szukać ciekawych posadzek? Najprościej na ulicy. Czy potrafisz odnaleźć wszystkie prezentowane niżej wzory na wrocławskich trotuarach? Czasem warto też obejrzeć parkiet w mieszkaniu znajomych, zajrzeć do starych kamienic, kościołów lub innych budynków. Zapraszamy do obejrzenia galerii i do własnych poszukiwań interesujących parkietaży. Nadesłane zdjęcia chętnie opublikujemy.

Niby taka prosta figura, a zauważcie, ile daje możliwości skomponowania parkietażu.

Czy potrafisz opisać, w jaki sposób przekształcono prostokąt, aby otrzymać kształty poniższych kostek brukowych?

Można zauważyć, że pionowe rozcięcie płytki  z piątego z kolei zdjęcia daje parkietaż archimedesowy z kwadratów i ośmiokątów - jeden z prezentowanych niżej.

Ciekawe możliwości daje połączenie prostokątów kilku rodzajów (w tym prostokąta z kwadratem), a także z dwunastokątem wklęsłym w kształcie krzyża greckiego.

Wydaje się, że parkietaż wykonany z kwadratów musi być bardzo prosty i niczym nie może nas zaskoczyć.

Wystarczy jednak wykorzystać kwadraty dwóch rodzajów, aby uzyskać niezwykle ciekawy matematycznie wzór. Taki chodnik można zobaczyć w kilku miejscach na ul. Sienkiewicza we Wrocławiu, m.in. przed Szkołą Podstawową nr 91. Zauważcie, że kwadraty wypełnią w ten sposób płaszczyznę niezależnie od rozmiarów ciemnej kostki. Ponadto parkietaż ten stanowi geometryczny dowód twierdzenia Pitagorasa. Dlaczego?

Bok pomarańczowego kwadratu z rysunku wyżej stanowi przeciwprostokątną trójkąta prostokątnego. Kostki chodnika są kwadratami zbudowanymi na przyprostokątnych tego trójkąta. Można zauważyć, że suma pól jasnego i ciemnego kwadratu daje pole kwadratu pomarańczowego. 

Parkietaże w pierwszym rzędzie dają złudzenie optyczne sześciennych kostek ustawionych jedne na drugich na różne sposoby. Zdjęcia drugie i trzecie przedstawiają ten sam układ, ale wrażenie jest znacznie silniejsze w przypadku trzeciego zdjęcia, na którym romby są w różnych kolorach. Parkietaż na zdjęciu czwartym również jest nietypowy - ma symetrię gwiaździstą.

Parkietaż na trzecim zdjęciu jest właściwie zbudowany z trapezów równoramiennych stanowiących połówki foremnego sześciokąta. Fotografię tę wykonano we wrocławskiej katedrze.

Pierwsze zdjęcie zostało wykonane na cmentarzu Père Lachaise w Paryżu (grobowiec Abelarda i Heloizy), a drugie to fragment dachu w niemieckiej Kleinwelce koło Budziszyna.

Parkietaż z pierwszego zdjęcia z sześciokątów foremnych i rombów jest powtórzony na drugim zdjęciu, ale obie płytki zostały zmodyfikowane. Ciekawy jest parkietaż ze zdjęcia trzeciego. Składa się z kwadratowych płytek w trzech rozmiarach oraz sześciokątów nieforemnych.

To ciekawy parkietaż z nieforemnych sześciokątów i pięciokątów z cmentarza Père Lachaise w Paryżu.

Ośmiokąty w tych parkietażach są foremne, zatem są to parkietaże półforemne (zwane też, w analogii do wielościanów półforemnych, archimedesowymi). Użyto do nich tylko wielokątów foremnych (dwóch rodzajów). Wszystkie przedstawiają ten sam układ figur.

A ośmiokąty w tych parkietażach nie są foremne (dlaczego?). Zatem nie są to parkietaże półforemne. Ciekawy jest ten, z ostatniego zdjęcia - można nań patrzeć także jako na parkietaż a) z kwadartów i nieforemnych pięciokątów, b) z kwadratów i nieforemnych sześciokątów lub c) z kwadratów i wklęsłych dwunastokątów w kształcie greckiego krzyża.

Efektowne parkietaże można łatwo uzyskiwać z form podstawowych, wprowadzając na płytce pewien ornament. Układając parkietaż np. z płytek trójkątnych lub rombowych z prostym ornamentem, otrzymuje się często nieoczekiwane desenie.

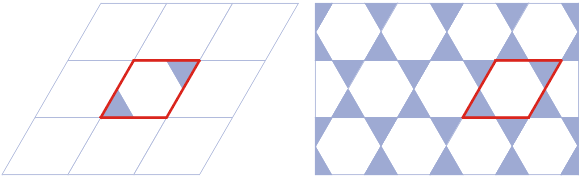
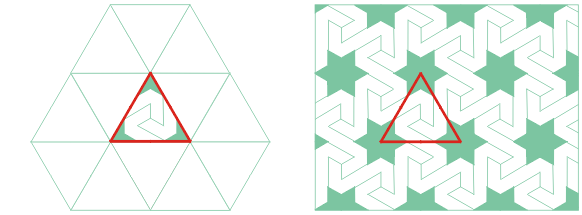
Poniższe posadzki wykonano z płytek kwadratowych z ornamentem. Czy potrafisz wskazać na nich formę podstawową?