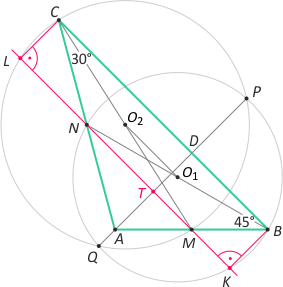
Zad. 1. W trójkącie ABC kąt B ma miarę 45°, a kąt C - 30°. Na środkowych BN i CM jako na średnicach zbudowano okręgi przecinające się w punktach P i Q. Cięciwa PQ przecina bok BC w punkcie D. Oblicz |BD|:|DC|.
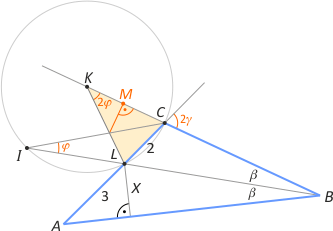
Zad. 2. W trójkącie ABC kąt C jest rozwarty. Dwusieczna BL dzieli bok AC na odcinki o długościach |AL|=3 i |LC|=2. Punkt K leżący na przedłużeniu boku BC poza wierzchołek C jest środkiem okręgu przechodzącego przez C, L i punkt przecięcia dwusiecznej BL z dwusieczną kąta ACK. Oblicz odległość punktu L od boku AB.
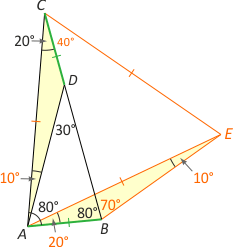
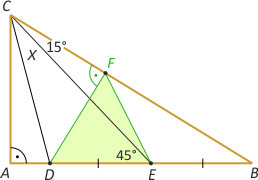
Zad. 3. W trójkącie ABC kąt A prosty. Na boku AB leży punkt E taki, że |∡ECB|=15°, oraz D taki, że |DE|=|EB|. Wiedząc, że |∡AEC|= 45°, oblicz miarę kąta DCE.
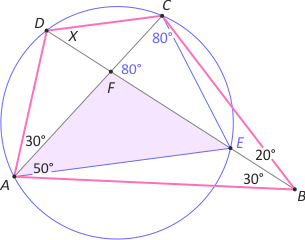
Zad. 4. (wolna amerykanka) W czworokącie wypukłym ABCD mamy: |∡DAC|=30°, |∡CAB|= 50°, |∡ABD|= 30° i |∡DBC|=20°. Oblicz miarę kąta BDC.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 - Mikołaj Popek (student UAM) i Szymon Kaźmierowski (nauczyciel z Elbląga),
- 28 - Iwona Gruszecka (nauczycielka z CLV LO w Warszawie),
- 22 - Elżbieta Grzechnik (emerytowana nauczycielka z Radomia) i Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 20 - Marzena Wąsiewicz (nauczycielka z Kajetan),
- 12 - Janusz Wieczorek (emerytowany nauczyciel z Sandomierza).
Za zadanie 4 po 10 pkt. otrzymali: Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek, Marzena Wąsiewicz, Szymon Kaźmierowski, Janusz Wieczorek oraz Szymon Meyer (analityk danych z Dziewkowic).
Gratulacje!
Zad. 1. Zauważmy, że prosta MN jest równoległa do BC, bo zawiera linię środkową MN trójkąta ABC. Łatwo wykazać, że odcinek O1O2 leży na linii średniej trapezu BCNM, a tym samym jest też równoległy do BC. Z kolei prosta PQ jest prostopadła do O1O2 (bo czworokąt QO1PO2 jest deltoidem), a tym samym jest prostopadła do BC. Niech prosta MN przecina okręgi w punktach K i L, a prostą PQ w punkcie T. Zauważmy, że kąty K i L są proste (jako wpisane oparte na średnicach), zatem czworokąt LKBC jest prostokątem. Z twierdzenia o cięciwach okręgu mamy |PT|·|TQ| = |NT|·|TK| oraz |PT|·|TQ| = |LT|·|TM|, skąd |NT|·|TK| = |LT|·|TM|. Uwzględniając że |TL| = |DB| i |KT| = |CD|, otrzymujemy |NT|·|CD| = |DB|·|TM| i mamy proporcję |DB|:|DC| = |NT|:|TM|, z której wynika, że prosta PQ przechodzi przez wierzchołek A. Otrzymaliśmy dwa trójkąty: ABD równoramienny, w którym |DB| = |AD|, i ekierkowy ADC. Ostatecznie |DB|:|DC| = |AD|:|DC| = 1/√3 = √3/3.
Zad. 2. Oznaczmy |∡K|=2φ i |∡C|=2γ. Wówczas kąt CIL ma miarę φ, bo jest wpisany w okrąg i oparty na tym samym łuku, co kąt K. Zauważmy, że kąt KCI jest zewnętrzny w trójkącie IBC, czyli γ=β+φ i β=γ–φ. Z kolei kąt ACK jest zewnętrzny w trójkącie ABC, więc 2γ = |∡A| + 2(γ–φ), skąd |∡A|=2φ. Oznacza to, że trójkąty ABL i LBK są przystające (z cechy kbk) i |LK|=|AL|= 3. Szukaną odległość znajdziemy jako wysokość w trójkącie równoramiennym LCK. Ze wzoru Herona PLCK=2√2, skąd LM=x=4√2/3.
Zad. 3. Niech F będzie takim punktem na boku BC, że kąt DFB jest prosty. Łatwo zauważyć, że |∡B|=45°–15°=30°. Otrzymaliśmy trójkąt ekierkowy DBF, w którym |DF|=|DB|/2 i |∡D|=60°. Oznacza to, że trójkąt DEF jest równoboczny i |∡EFB|=180°–90°–60°=30°. Jest on zewnętrzny w trójkącie EFC, skąd |∡CEF|=15° i |EF|=|FC|. Z równości |EF|=|DF| wynika, że trójkąt DFC jest równoramienny i prostokątny, zatem |∡X|=45°–15°=30°.
Zad. 4. Zapoznajmy się z ciekawym faktem dotyczącym trójkąta równoramiennego o kącie przy wierzchołku 20°. Jeśli obrać na boku BC punkt D taki, że |∡DAB|=70°, to |AB|=|DC|. Niech E będzie takim punktem, że trójkąt AEC jest równoboczny. Łatwo zauważyć, że trójkąty ABE i ADC są przystające i |AB|=|DC| (patrz rysunek). Wykorzystamy ten fakt w rozwiązaniu zadania. Opiszmy na trójkącie ACD okrąg. Przecina on odcinek BD w punkcie E. Kąt CFB jest zewnętrzny w trójkącie AFB, więc |∡CFB|=80° oraz |∡CEF|=30° (bo jest wpisany i oparty na tym samym łuku co kąt DAC), zatem |∡FCE|=70° i na mocy dowiedzionego wcześniej faktu |CF|=|EB|. Wystarczy teraz zauważyć, że z równoramienności trójkątów ABC i FBC wynika, że |AF|=|AC|–|FC|=|FB|–|EB|, co oznacza, że trójkąt AEF jest równoramienny o kącie przy wierzchołku |∡F|=100°. Szukany kąt jest oparty na tym samym łuku co kąt CAE i ma miarę 40°.