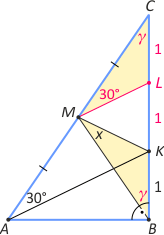
Zad. 1. W trójkącie ABC kąt B jest prosty, M to środek boku AC, a K to punkt na boku BC taki, że |BK|=1 i |KC|=2. Wiedząc, że miara kąta CAK wynosi 30°, znajdź miarę BMK.
Zad. 2. Dany jest kwadrat ABCD. Niech E będzie środkiem boku BC. Na odcinku DE obrano punkt F taki, że |AF|=|AD|. Wiedząc, że pole trójkąta AFD wynosi 8, oblicz pole kwadratu.
Zad. 3. Dany jest kwadrat ABCD. Na boku DC obrano punkt E. Odcinki AC i BE przecinają się w punkcie O. Wiedząc, że pola trójkąta OBC wynosi 6, a czworokąta AOED - 11, oblicz pole kwadratu.
Zad. 4. (wolna amerykanka) W trapezie ABCD mamy |∡DCA|= 2|∡DBA|, |DC|=|CA|=13/2 oraz
|AB|=12. Oblicz pole trapezu.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 - Iwona Gruszecka (nauczycielka w CLV LO Warszawa), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia), Marzena Wąsiewicz (nauczycielka z Kajetan), Janusz Wieczorek (emerytowany nauczyciel z Sandomierza) oraz Szymon Kaźmierowski (nauczyciel z Elbląga),
- 28 - Igor Sudyka (uczeń V LO Kraków).
Za zadanie 4 po 10 pkt. otrzymali: Elżbieta Grzechnik, Iwona Gruszecka, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek, Marzena Wąsiewicz, Igor Sudyka, Szymon Kaźmierowski, Janusz Wieczorek oraz Szymon Meyer (analityk danych z Dziewkowic).
Gratulujemy!
Zad. 1. Niech punkt L będzie środkiem boku BC. Odcinek ML jest linią średnią w trójkącie AKC, stąd |∡LMC| = 30°. Dalej |BM| = |MC| z własności środkowej przeciwprostokątnej w trójkącie ABC, zatem trójkąty MLC i BKM są przystające (z cechy bkb). Ostatecznie |∡BMK| = 30°.
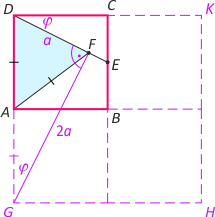
Zad. 2. Zauważmy, że kąt GFD jest prosty, bo punkty G, F i D leżą na okręgu o środku w punkcie A. PDGF = 16. Trójkąty DCE i DGF są podobne w skali k = |CE|:|CD| = |DF|:|FG| = 1/2. Otrzymujemy PDGF = 16 = a2, skąd a = 4 i |DG| = √80. Pole kwadratu GHKD wynosi 80, a pole ABCD wynosi 20.
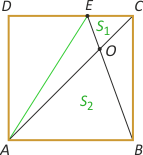
Zad. 3. Skorzystamy z własności czworokąta PABO . PEOC = PAOE · PBOC. Otrzymujemy równanie (1/2PABCD – 11)·(1/2PABCD – 6) = 36, skąd PABCD = 30.
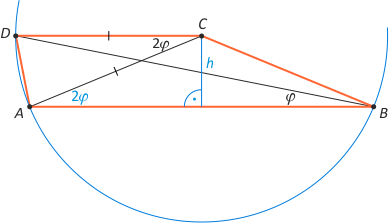
Zad. 4. Łatwo zauważyć, że punkty D, A i B leżą na okręgu o środku w punkcie C. Z twierdzenia Pitagorasa w równoramiennym trójkącie ABC mamy h = 5/2 i
ostatecznie pole trapezu P = 185/5.
