Inna nazwa:
wzór Regiomontana
Sformułowanie:
W dowolnym trójkącie stosunek sumy do różnicy długości dwóch boków jest taki sam, jak stosunek tangensów połowy sumy i połowy różnicy przeciwległych kątów, tzn. zachodzi:
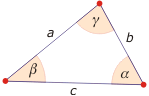
$$\frac{a+b}{a-b} = \frac{\tan{\frac{\alpha + \beta}{2}}}{\tan{\frac{\alpha - \beta}{2}}} \ .$$
Dowód:
Powyższą zależność łatwo wykazać, korzystając z twierdzenia sinusów, z którego mamy:
a = 2Rsinα i b = 2Rsinβ. Podstawiając te wielkości do lewej strony wzoru, otrzymujemy:
$$\frac{a+b}{a-b} = \frac {2R \sin \alpha + 2R \sin \beta}{2R \sin \alpha - 2R \sin \beta} = \frac{\sin \alpha + \sin \beta}{\sin \alpha - \sin \beta} \ . $$
Korzystając teraz ze wzorów na sumę i różnicę sinusów oraz z tożsamości $\tan x= \frac{\sin x}{\cos x}$, otrzymujemy dalej:
$$\frac {2 \sin {\frac {\alpha + \beta}{2}} \cos{\frac{\alpha - \beta}{2}}} {2 \cos {\frac {\alpha + \beta}{2}} \sin{\frac{\alpha - \beta}{2}}} = \frac{\tan{\frac{\alpha + \beta}{2}}}{\tan{\frac{\alpha - \beta}{2}}} \ .$$
- Niemiecki astronom i matematyk Regiomontanus w XV w. używał tego wzoru do obliczeń, które pomogły mu uporządkowac trygonometrię płaską i sferyczną oraz sporządzić tablice trygonometryczne.
- twierdzenie sinusów
- twierdzenie kosinusów
- trygonometria



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
