Inna nazwa:
twierdzenie Snelliusa
Sformułowanie:
Stosunek długości dowolnego boku trójkąta do sinusa przeciwległego kąta jest stały i równy podwojonej długości promienia R okręgu opisanego na tym trójkącie, tzn.
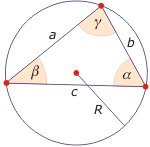$$\frac{ a}{ \sin \alpha} = \frac{ b}{ \sin \beta} = \frac{ c}{ \sin \gamma} =2R$$
Dowód:
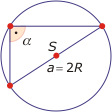
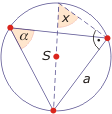
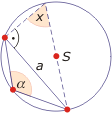
Korzystając ze wzoru na pole trójkąta, mamy 1/2 absinγ = 1/2 acsinβ = 1/2 bcsinα. Mnożąc przez 2 i dzieląc przez abc otrzymamy sinγ/c = sinβ/b = sinα/a. Wystarczy teraz wziąć odwrotności tych liczb. Trzeba jeszcze udowodnić, że a/sinα = 2R. Wynika to z poniższych rysunków.
Zastosowania:
- Obliczanie rozwartości kątów trójkąta, gdy dane są długości dwóch boków dwóch boków i rozwartość jednego kąta.
- Obliczanie długości boków trójkąta, gdy dane są rozwartości dwóch kątów i długość jednego boku.
Uogólnienia:
- Wersja przestrzenna - w czworościanie o krawędziach długości a, b, c wychodzących z jednego wierzchołka i o odpowiednio do nich skośnych krawędziach długości a', b', c', oznaczmy przez $\angle$x kąt między ścianami spotykającymi się wzdłuż krawędzi x. Wtedy zachodzi:
$$\frac{\sin \angle a \cdot \sin \angle a'}{aa'} = \frac{\sin \angle b \cdot \sin \angle b'}{bb'} = \frac{\sin \angle c \cdot \sin \angle c'}{cc'} \ .$$ -
Wersja na sferze - w trójkącie sferycznym o bokach (tzn. łukach okręgów wielkich) długości a, b, c (długość łuku jest więc kątem w radianach) i kątach dwuściennych leżących naprzeciw tych boków α, β, γ, zachodzi:
$$\frac{\sin \alpha}{\sin a} = \frac{\sin \beta}{\sin b} = \frac{\sin \gamma}{\sin c} \ . $$
rysunek
- Na początku XVII w. holenderski matematyk Willebrord Snell (zwany też Snelliusem) stosował to twierdzenie do obliczania odległości między punktami na kuli ziemskiej metodą triangulacji. Wyniki te wykorzystał potem do wyliczenia promienia Ziemi.
- rozwiązywanie trójkątów
- twierdzenie kosinusów
- twierdzenie tangensów
- trygonometria
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
