ROZMAITOŚCI › Leksykon matematyczny

Twierdzenie kosinusów

Data ostatniej modyfikacji:
2018-09-18
Autor: 
Sebastian Guz
student matematyki UWr
Dział matematyki: 
geometria analityczna
geometria syntetyczna
Pojęcia podstawowe 

Inne nazwy:

Sformułowania:

  • W dowolnym trójkącie kwadrat długości jednego boku jest równy sumie kwadratów długości pozostałych dwóch boków pomniejszonej o podwojony iloczyn długości tych boków i kosinusa kąta zawartego między nimi, tzn:

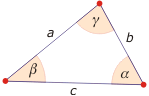$$a^2 = b^2 + c^2 - 2bc \cdot \cos \alpha \ ;$$

$$b^2 = a^2 + c^2 - 2ac \cdot \cos \beta \ ;$$

$$c^2 = a^2 + b^2 - 2ab \cdot \cos \gamma \ .$$

 

  • W dowolnym trójkącie pole kwadratu zbudowanego na jednym boku jest równe sumie pól kwadratów zbudowanych na pozostałych bokach pomniejszonej o iloczyn pola prostokąta o tych właśnie bokach i kosinusa kąta, jaki jest w trójkącie między nimi. 

Dowód:
Twierdzenie kosinusów można łatwo wykazać, korzystając z twierdzenia Pitagorasa.

 

 

 

 

 a2 =
= c12+ h2 = (c-c2)2+ (b2-c22) = c2+ b2- 2cc2 = c2+ b2- 2bc·c2/b =
= c2+ b2- 2bccosα

Analogiczne rozumowanie trzeba jeszcze przeprowadzić w przypadku wysokości spadającej na przedłużenie boku. 

Zastosowania:

  • Obliczanie długości trzeciego boku trójkąta, gdy znane są długości pozostałych boków i rozwartość kąta między nimi.
  • Obliczanie kątów trójkąta, gdy znane są długości jego boków.

Uogólnienia:

  • Wersja przestrzenna - w dowolnym czworościanie o wierzchołkach A, B, C, D przez PX oznaczmy pole ściany leżącej naprzeciw wierzchołka X, a przez $\angle$XY oznaczmy kąt między ścianami leżącymi naprzeciw wierzchołków X i Y; wtedy zachodzi:

    PA2 = PB2 + PC2 + PD2  -  2PBPCcos$\angle$BC  -  2PBPDcos$\angle$BD  -  2PCPDcos$\angle$CD .

  • Wersja na sferze - w trójkącie sferycznym o bokach (tzn. łukach okręgów wielkich) długości a, b, c (długość łuku jest więc kątem w radianach) i kącie dwuściennym γ leżącym pomiędzy bokami a i b, zachodzi:
    cos c  =  cos a · cos b  +  sin a · sin b · cos γ.

rysunek

 

Historia
  • Szczególny przypadek twierdzenia kosinusów dla kąta prostego nazywamy twierdzeniem Pitagorasa. Jego dowód podano w starożytnej Grecji w VI w. p.n.e.
  • Ogólne twierdzenie udowodnił w XVIII w. francuski matematyk i polityk Lazare Carnot, jeden z twórców nowoczesnej geometrii.
  • Na przełomie XVIII i XIX w. niemiecki matematyk Karol Gauss wykazał, że twierdzenie kosinusów jest twierdzeniem geometrii euklidesowej i nie zachodzi w geometriach nieeuklidesowych (np. na sferze).  
Terminy pokrewne

 

‹ Torusw góręTwierdzenie Pitagorasa ›

Powrót na górę strony