Do boju z Pitagorasem

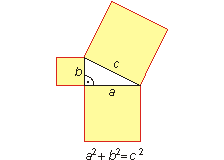
Twierdzenie Pitagorasa to jeden z pierwszych doniosłych faktów geometrycznych, jakie poznaje się w szkole. Wcześniej lekcje geometrii przypominają naukę trudnych słówek w języku obcym, albo polegają na obliczaniu pól, obwodów i objętości, a to wcale nie jest geometria! Geometria to piękno i prostota dedukcyjnych rozumowań oraz możliwość zastosowania teorii do opisywania otaczającej nas rzeczywistości.

Przypomnij sobie treść twierdzenia Pitagorasa. Czy potrafisz to twierdzenie uzasadnić? A jak brzmi twierdzenie odwrotne? Czy jest prawdziwe? Jeśli nie pamiętasz, znajdziesz pomoc w portalowym Leksykonie matematycznym.

Oto kilka dowodów twierdzenia Pitagorasa. Uzasadnij równości odpowiednich pól.

Pamiętaj, że we wszystkich zadaniach praktycznych konieczne jest przyjęcie dodatkowych założeń, które idealizują rzeczywistość, ale jednocześnie umożliwiają zastosowanie w rozwiązaniach metod matematycznych. Bowiem matematyka działa tylko na modelach, a nie na rzeczywistych obiektach, a naszym celem jest znalezienie modeli jak najwierniej odzwierciedlających rzeczywistość.
Wyobraź sobie sytuację opisaną w każdym zadaniu, naszkicuj ją i zaznacza trójkąt prostokątny, z którego własności chcesz skorzystać.

Sytuacje płaskie

1. Dziadek Aleks kupił od Zarządu Ogródków Strawbery Fields Forever kwadratową działkę rekreacyjną. Zmierzył alejki biegnące wzdłuż jej przekątnych i otrzymał w sumie 80 m. Ile metrów bieżących siatki potrzebuje dziadek na ogrodzenie swojej działki? Dziadek Aleks postanowił obsadzić całą działkę truskawkami odmiany Mucha nie siada, które uwielbiają jego wnuki. W celu optymalnego nasłonecznienia na każdym metrze kwadratowym powinno rosnąć nie więcej niż 40 sadzonek. Ile sadzonek dziadek powinien zakupić?

2. Ogród różany hrabiny Cosel ma kształt trójkąta równobocznego o boku 1200 m. W jego wierzchołkach biją trzy cudowne źródła. W sercu ogrodu romantyczna hrabina pragnie wybudować Altanę westchnień, ale w takim miejscu, by leżała w równych odległościach od każdego ze źródeł. Jak długą drogę będzie musiała pokonać z altany, by napić się źródlanej wody?

3. Pomysłowy Dobromir skleił czworokątny latawiec z dwóch trójkątów prostokątnych, stykając je bokami o długości 50 cm. W jednym trójkącie bokiem tym była przyprostokątna, a w drugim przeciwprostokątna. Pewne przyprostokątne w tych trójkątach miały odpowiednio 120 cm i 40 cm. Jaki był obwód latawca?

4. Huragan Helmans wyrządził wiele szkód. Uszkodził m.in. tysiącletnią stumetrową sekwoję tak, że częściowo przełamała się na pewnej wysokości a jej wierzchołek sięgnął ziemi w odległości 40 m od pnia drzewa. Na jakiej wysokości Helmans przełamał drzewo?

5. Wokół prostokątnego ogrodu jordanowskiego wykopano kanał o szerokości 4 m, po którym można pływać kajakami. Z kolei wzdłuż zewnętrznego brzegu kanału poprowadzono alejkę, na której postawiono budkę z lodami i drugą z watą cukrową. Stoją one na sąsiednich bokach alejki w odległości 120 m i 160 m od ich wspólnego wierzchołka. Przed każdą z nich przerzucono mostek nad kanałem prowadzący na teren ogrodu. Która droga między budkami z łakociami jest krótsza: wzdłuż alejki, czy wiodąca przez dwa mostki i na skróty przez ogród?

Proste sytuacje przestrzenne

1. Dom Capulettich stoi frontem do ulicy via d'Amor o szerokości 3 m (razem z chodnikami). Krawędź balkonu Julii znajduje się na wysokości 4 m nad ziemią. Romeo przyniósł 5 metrową drabinę, którą chce ustawić tak, by jej górny koniec sięgał dokładnie do krawędzi balkonu. Jak daleko od ściany domu Capulettich powinien ustawić dolny koniec drabiny? Czy via d'Amor nie jest zbyt wąska, by mu się to udało?

2. Dom Ani z Green Hill leży 80 m, a dom Diany 60 m od rzeki, ale na przeciwnych brzegach. Na wysokości każdego z domów przerzucono przez rzekę mostek. Gdyby domy leżały na tym samym brzegu i w równej odległości od rzeki, dzieliłoby je 140 m. Rzeka ma 4 m szerokości. Jaką najkrótszą drogę musi pokonać Ania, by odwiedzić Dianę? A jaką Diana, by odwiedzić Anię?

3. Filias Fogg podróżuje w balonie na wysokości 150 m nad Równiną Filozofów. Właśnie przelatuje nad pomnikiem Pomponidasa, będąc jednocześnie w odległości 170 m od podstawy cokołu pomnika Mamałazjasza. Jaka jest odległość między pomnikami?

4. Zosia Samosia rysuje okrąg o promieniu 5 cm cyrklem o ramionach długości 13 cm, trzymając go w płaszczyźnie prostopadłej do płaszczyzny kartki. Cyrkiel zwieńczony jest kulką o średnicy 1 cm. W jakiej odległości od kartki znajduje się czubek cyrkla?

5. W wiśniowym sadzie na drzewach rosnących w odległości 5 m siedzą Ptyś i Balbina. Chłopiec wdrapał się 2 m nad ziemię, a Balbina siedzi na wysokości 1 m. Pomiędzy drzewami ustawili wiadro tak sprytnie, że są od niego w jednakowych odległościach. Teraz jedzą wiśnie i celują pestkami do wiadra. Na jaką odległość muszą wystrzelić pestki?

1. Dwa ptaki wylatują w tym samym momencie ze szczytów dwóch wież odległych o 50 m. Wysokość jednej wieży to 30, a drugiej – to 40 m. Lecąc z tą samą prędkością, ptaki dolatują w tym samym momencie do fontanny usytuowanej na prostej łączącej podstawy obu wież. W jakich odległościach od wież znajduje się fontanna?

2. Oblicz obwód trójkąta, w którym dwa boki mają długości 1 i 2, a kąt między nimi ma 120 stopni.

3. Czworokąt ABCD jest wpisany w okrąg o średnicy d, a odcinki AC i BD są prostopadłe. Udowodnij, że AB² + CD² = d².

4. Na kwadratowej ścianie prostopadłościanu 4 na 4 na 10 siedzi pająk krzyżak. Jest w odległości 3 od jednego boku ściany, na której siedzi, i 2 od innego. Znajdź najkrótszą drogę, po której pająk może przedostać się na punkt położony symetrycznie do jego obecnego położenia względem środka prostopadłościanu.

5. Czy trójkąt o bokach długości $3-\sqrt{2}$ , $\sqrt{2}+3$ i $2\sqrt{5}$ jest prostokątny?