Wiadomo, że wypukłe wielościany foremne (tzw. bryły platońskie) muszą spełniać trzy warunki: a) ściany są wypukłymi wielokątami foremnymi, b) ściany są przystające, c) naroża są przystające. Istnieje tylko pięć takich wielościanów. Łatwo można sprawdzić, że jeśli zrezygnujemy z warunku c) przystawania naroży, to bryły wypukłe spełniające warunki a) i b) muszą mieć ściany w kształcie trójkątów równobocznych, których w poszczególnych wierzchołkach może schodzić się 3, 4 lub 5. Takie wielościany nazywamy wypukłymi deltościanami. Ich nazwa pochodzi od wielkiej greckiej litery delta, która ma kształt trójkąta. Ile wypukłych deltościanów potrafisz wskazać? A ile niewypukłych?
Trzy z deltościanów wypukłych są bryłami platońskimi. To foremny czworościan, ośmiościan i dwudziestościan. Istnieje jeszcze pięć innych deltościanów, które są wypukłe. Każdy z nich ma inną liczbę ścian (6, 10, 12, 14 i 16). Jest też nieskończenie wiele deltościanów niewypukłych. Wszystkie mają parzyste liczby ścian (dlaczego?) większe od 6 (dlaczego?) i każdą z tych liczb da się zrealizować jako liczbę ścian deltościanu (dlaczego?).
W technice origami łatwo wykonać dowolny deltościan, jeśli przygotujemy moduły w kształcie trójkąta równoramiennego. To kolejna propozycja dla niecierpliwych, zabieganych i początkujących. Przygotowanie modułów i ich łączenie jest bowiem bardzo proste. Łatwo też można rozmontować gotową bryłę, a te same moduły wykorzystywać do budowania innego modelu.
Więcej o deltościanach wypukłych możesz przeczytać na Portalu tutaj.
Jak wykonać pojedynczy moduł
Potrzebne są kartki w kształcie trójkątów równobocznych. Można je przygotować samemu lub kupić w bloczkach w niektórych sklepach papierniczych. Trzeba przygotować ich tyle, ile ścian będzie miała budowana bryła. Niestety, im więcej jest ścian, tym bardziej niestabilny staje się model.
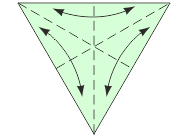
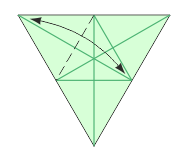
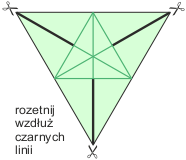
Jak łączyć moduły
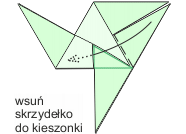
Moduły łączą się ze sobą nawzajem przez wsunięcie skrzydełka jednego z nich do kieszonki modułu z nim graniczącego i vice versa.
Z czterech splecionych modułów, powstaje gotowa ściana trójkątna (jej brzeg zaznaczono na poniższym rysunku białą linią). Cały rysunek przedstawia natomiast siatkę czworościanu. Można go zbudować, zaginając ściany i łącząc sąsiednie moduły (fioletowy z zielonym, zielony z pomarańczowym i pomarańczowy z fioletowym).
 |
 |
|
4-deltościan wypukły
czworościan foremny
|
Galeria deltościanów
(Po kliknięciu w nazwę bryły pojawi się dynamiczny rysunek, który można obracać za pomocą myszy.)
Po dołożeniu kolejnych dwóch modułów otrzymujemy siatkę złożoną z 6 ścian, a niej możemy złożyć wypukły sześciościan będący dwupiramidą trójkątną (to jakby dwa czworościany foremne sklejone podstawami).
 |
 |
 |
 |
|
6-deltościan wypukły
dwupiramida trójkątna
|
Po dodaniu jeszcze dwóch ścian możemy złożyć ośmiościan foremny będący dwupiramidą kwadratową, a po dodaniu kolejnych dwóch - dziesięciościan będący dwupiramidą pieciokątną.
 |
 |
|
8-deltościan wypukły
ośmiościan foremny, czyli
dwupiramida kwadratowa, czyli
graniastosłup trójkątny skręcony
|
10-deltościan wypukły
dwupiramida pięciokątna
|
A jak zbudować 8-deltościan i 10-deltościan wklęsły? Czy takie bryły są unikatowe? Czy można zbudować kilka nieprzystających egzemplarzy?
Aby otrzymać 8-deltościan wklęsły wystarczy dokleić czworościan foremny do jednej ściany dwupiramidy trójkatnej. Powstająca bryła nie jest wypukła (kąt dwuścienny czworościanu to ok. 70,5°, a jego trzykrotność daje kąt o mierze większej od 180°) i jest unikatowa. Doklejenie do niej kolejnego czworościanu daje wklęsły 10-deltościan. Oczywiście w zależności od wyboru podstawy pod doklejany czworościan można uzyskać 10-deltościany różnych kształtów.
 |
 |
|
8-deltościan wklęsły
dwupiramida trójkątna powiększona
|
10-deltościan wklęsły
dwupiramida trójkątna dwukrotnie powiększona
|
Z 12 trójkątnych ścian możemy złożyć deltościan wypukły i kilka wklęsłych. Wypukły powstaje przez rozcięcie dwóch sąsiednich krawędzi z talii dwupiramidy pięciokątnej i wstawienie w to miejsce dwóch trójkątów. Wklęsły otrzymamy np. po doklejeniu czworościanu do każdej ze ścian czworościanu foremnego. Można by sądzić, że wypukły 12-deltościan otrzymamy także po doklejeniu czworościanów foremnych do dwóch równoległych ścian ośmiościanu foremnego. Tak się jednak nie stanie, gdyż powstała bryła w ogóle nie będzie deltościanem. Kąty dwuścienne uzupełnią się do półpełnego i powstanie równoległościan (dwa sąsiednie trójkąty utworzą ścianę w kształcie rombu).
 |
 |
|
12-deltościan wypukły
|
12-deltościan wklęsły
czterokrotnie powiększony czworościan foremny
|
Wypukły deltościan o 14 ścianach powstanie z doklejenia piramid kwadratowych do ścian bocznych graniastosłupa trójkątnego, zaś deltościan wklęsły o 14 ścianach to np. sklejone ścianami dwa ośmiościany foremne (tzn. sklejone podstawami dwa graniastosłupy skręcone trójkątne).
 |
 |
|
14-deltościan wypukły
|
14-deltościan wklęsły
granistosłup trójkątny skręcony podwójny
|
Wypukły deltościan o 16 ścianach powstanie z doklejenia piramid kwadratowych do podstaw graniastosłupa kwadratowego skręconego. A wklęsły powstanie np. z doklejenia piramid (trzech kwadratowych i jednej trójkątnej) do ścian bocznych i jednej podstawy graniastosłupa trójkątnego.
 |
 |
|
16-deltościan wypukły
|
16-deltościan wklęsły
poczwórnie powiększony granistosłup trójkątny
|
Może się to wydać dziwne, ale nie istnieje deltościan wypukły o 18 ścianach. A czy istnieje wklęsły? Oczywiście tak. Można go otrzymać, np. doklejając piramidy (kwadratowe lub trójkątne) do odpowiednich ścian graniastosłupa trójkątnego.
Deltościan wypukły o 20 ścianach to ostatni z wielościanów platońskich - dwudziestościan foremny (powstaje z doklejenia piramid pięciokątnych do podstaw graniastosłupa pięciokątnego skręconego), zaś deltościan wklęsły o 20 ścianach to np. trzy sklejone ośmiościany foremne (tzn. trzy sklejone podstawami graniastosłupy skręcone trójkątne).
 |
 |
|
20-deltościan wypukły
dwudziestościan foremny
|
20-deltościan wklęsły
graniastosłup trójkątny skręcony potrójny
|
Deltościany o więcej niż 20 ścianach są wszystkie niewypukłe, np. gwiazda 8-ramienna (stella octangula), która powstaje z doklejenia czworościanu do każdej ze ścian ośmiościanu foremnego, lub gwiazda 6-ramienna, która powstaje z doklejenia piramidy czworokątnej do każdej ze ścian sześcianu.
 |
 |
|
24-deltościan
stella octangula, czyli
ośmiokrotnie powiększony ośmiościan foremny
|
24-deltościan
sześciokrotnie powiększony sześcian
|
Deltościanów wklęsłych jest nieskończenie wiele. Mogą mieć dowolną parzystą liczbę ścian. Wystarczy do jednej ściany n-deltościanu dokleić czworościan formeny, otrzymując n+2-deltościan. Czy taka konstrukcja jest zawsze geometrycznie wykonalna? Deltościany o liczbie ścian przekraczającej zadaną wielkość można budować np. przez sklejanie podstawami dowolnej liczby graniastosłupów skręconych trójkątnych (czyli ośmiościanów foremnych) lub graniastosłupów skręconych czworo- albo pięciokątnych, które zaklejamy na obu końcach odpowiednimi piramidami.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
