Wzory skróconego mnożenia

Data ostatniej modyfikacji:
2018-09-14

Wzory skróconego mnożenia są przydatne przy mnożeniu lub potęgowaniu wyrażeń algebraicznych. Często ułatwiają sprawne rachunki. Takich wzorów jest bardzo dużo. Poniżej podajemy kilka, z których korzysta się najczęściej.

Kwadrat sumy liczb

(a + b)²= a²+ 2ab + b²na przykład: 31²= (30+1)²= 30²+2×30+1 = 900+60+1 = 961
nie zachodzi równość: (a+b)² = a² + b²na przykład 25 = (3+2)² $\color{\red} \neq$ 3² + 2²= 13
uzasadnienie wzoru przez rachunek:
(a + b)²= (a + b) × (a + b)= mnożymy każdy wyraz przez każdy inny
= aa+ ab + ba + bb = a²+ 2ab + b²
uzasadnienie wzoru przez rysunek:

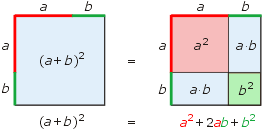
Kwadrat różnicy liczb

(a - b)²= a²- 2ab + b²na przykład: 29²= (30-1)²= 30²-2×30+1 = 900-60+1 = 841
nie zachodzi równość: (a-b)² = a² - b²na przykład 1 = (3-2)² $\color{\red} \neq$ 3² - 2²= 5
uzasadnienie wzoru przez rachunek:
(a - b)²= (a - b) × (a - b)= mnożymy każdy wyraz przez każdy inny
= aa- ab - ba + bb = a²- 2ab + b²
uzasadnienie wzoru przez rysunek:

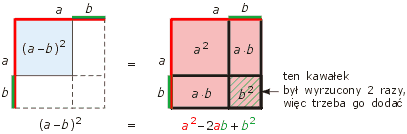
Kwadrat sumy trzech liczb

(a+b+c)²= a²+ b²+ c²+ 2ab + 2ac + 2bc
na przykład: 111²= (100+10+1)²= 100²+ 10²+1 +2×100×10 + 2×100 + 2×10 =
= 10000 + 100 + 1 + 2000 + 200 + 20 = 12321
nie zachodzi równość: (a+b+c)² = a² + b²+ c²na przykład 36 = (3+2+1)² $\color{\red} \neq$ 3² + 2²+ 1² = 14
uzasadnienie wzoru przez rachunek:
(a + b + c)²= (a + b + c) × (a + b + c)= mnożymy każdy wyraz przez każdy inny
= aa+ ab + ac + ba + bb + bc + ca + cb + cc = a²+ b²+ c²+ 2ab + 2ac + 2bc
uzasadnienie wzoru przez rysunek:

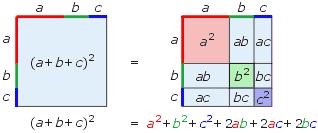
Iloczyn sumy i różnicy liczb = Różnica kwadratów liczb

(a + b)×(a - b) = a²- b²na przykład: 101×99 = (100+1)×(100-1) = 100²- 1 = 9999
uzasadnienie wzoru przez rachunek:
(a + b) × (a - b)= mnożymy każdy wyraz przez każdy inny
=aa- ab + ba - bb = a²- b²
uzasadnienie wzoru przez rysunek: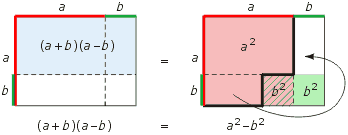

Sześcian sumy liczb

(a + b)³= a³+ 3a²b + 3ab²+ b³na przykład: 101³= (100+1)³ =100³+ 3×100²+ 3×100 + 1 =
= 1000000 + 30000 + 300 + 1 = 1030301
nie zachodzi równość: (a+b)³ = a³ + b³na przykład 125 = (3+2)³ $\color{\red}\neq$ 3³ + 2³= 35
uzasadnienie wzoru przez rachunek:
(a + b)³= (a + b) × (a + b) × (a + b)= mnożymy każdy wyraz przez każdy inny
= (aa+ ab + ba + bb) × (a + b) = aaa+ aab + aba + abb + baa+ bab + bba + bbb =
= a³+ 3a²b + 3ab²+ b³
uzasadnienie wzoru przez rysunek:

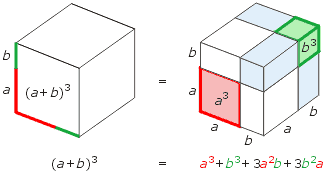
Sześcian różnicy liczb

(a - b)³= a³- 3a²b + 3ab²- b³na przykład: 99³ = (100-1)³ = 100³- 3×100²+ 3×100 - 1 =
= 1000000 - 30000 + 300 - 1 = 970299

n-ta potęga sumy

Według poniższego wzoru możemy obliczyć dowolną naturalną potęgę sumy dwóch liczb:

[TEX](a+b)^n={{n}\choose{0}}a^n+{{n}\choose{1}}a^{(n-1)}b+{{n}\choose{2}}a^{(n-2)}b^2+...+{{n}\choose{n-1}}ab^{(n-1)}+{{n}\choose{n}}b^n[/TEX]

Należy tylko pamiętać jak obliczamy symbol Newtona: [tex]{{n}\choose{k}}=\frac{n!}{{k!}{(n-k)!}}[/tex].

W ustaleniu współczynników przy iloczynach potęg składników sumy, której potęgę obliczamy może nam posłużyć trójkąt Pascala:

[TEX]\small \begin{array}{r|ccccccccccccccccccc} n \\ \hline 0&&&&&&&&&& 1 \\1&&&&&&&&&1&&1 \\2 &&&&&&&&1 & & 2 & &1 \\3 &&&&&&&1&&3&&3&&1 \\4 &&&&&&1 &&4&&6&&4&&1 \\5 &&&&&1 &&5&&10&&10&&5&&1 \\6 &&&&1 &&6&&15&&20&&15&&6&&1 \\7 &&&1 &&7&&21&&35&&35&&21&&7&&1 \\8 &&1&&8&&28&&56&&70&&56&&28&&8&&1 \\9 &1&&9&&36&&84&&126&&126&&84&&36&&9&&1\\\vdots &&&&&&&&&& \vdots \end{array}[/TEX]

Każda liczba w trójkącie jest sumą dwóch liczb znajdujących się bezpośrednio nad nią, przy czym zewnętrzne liczby w każdej linii to jedynki.

[tex]{{n}\choose{k}}[/tex] = k-ta liczba w n-tym wierszu trójkąta Pascala

na przykład:

[tex]12^4=(10+2)^4={{4}\choose{0}}\cdot10^4+{{4}\choose{1}}\cdot{{10}^{3}}\cdot{2^{1}}+{{4}\choose{2}}\cdot{{10}^{2}}\cdot{{2}^{2}}+{{4}\choose{3}}\cdot{{10}^{1}}\cdot{{2}^{3}}+{{4}\choose{4}}\cdot{{2}^{4}}=[/tex]

[tex]={{10}^{4}}+{4}\cdot{{10}^{3}}{2^{1}}+{6}\cdot{{10}^{2}}{{2}^{2}}+{4}\cdot{{10}^{1}}{{2}^{3}}+{{2}^{4}}=10000+8000+2400+320+16=20736[/tex]

n-ta potęga różnicy

Wystarczy zauważyć, że (a - b)ⁿ = [a + (-b)]ⁿ i zastosować powyższy wzór dla sumy. Wyrazy rozwinięcia pozostaną takie same, jedynie przed co drugim składnikiem znak "+" zmieni się na "-".
na przykład:

[tex]18^4=(20-2)^4={{4}\choose{0}}\cdot20^4-{{4}\choose{1}}\cdot{{20}^{3}}\cdot{2^{1}}+{{4}\choose{2}}\cdot{{20}^{2}}\cdot{{2}^{2}}-{{4}\choose{3}}\cdot{{20}^{1}}\cdot{{2}^{3}}+{{4}\choose{4}}\cdot{{2}^{4}}=[/tex]

[tex]={{20}^{4}}-{4}\cdot{{20}^{3}}{2^{1}}+{6}\cdot{{20}^{2}}{{2}^{2}}-{4}\cdot{{20}^{1}}{{2}^{3}}+{{2}^{4}}=160000-64000+9600-640+16=[/tex]

[tex]= 104976[/tex]

Suma sześcianów liczb

a³+ b³= (a + b)×(a²- ab + b²)

uzasadnienie wzoru przez rachunek (mnożymy każdy wyraz przez każdy inny):

(a + b)×(a²- ab + b²) = aa²- aab + ab²+ ba²- bab + bb²= a³ - a²b + ab²+ a²b - ab²+ b³ =
= a³ + b³

Różnica sześcianów liczb

a³- b³= (a - b)×(a²+ ab + b²)

uzasadnienie wzoru przez rachunek (mnożymy każdy wyraz przez każdy inny):

(a - b)×(a²+ ab + b²) = aa²+ aab + ab²- ba²- bab - bb² = a³ + a²b + ab²- a²b - ab²- b³ =
= a³ - b³

Różnica czwartych potęg liczb

a⁴- b⁴= (a - b)×(a³+ a²b + ab² + b³) = (a + b)×(a³ - a²b + ab² - b³)

Suma n-tych potęg liczb (dla n nieparzystych!!!)

aⁿ + bⁿ = (a + b) (aⁿ^-1 - aⁿ^-2b + aⁿ^-3b² - ... + bⁿ^-1)

Różnica n-tych potęg liczb (dla n parzystych!!!)

aⁿ - bⁿ = (a + b) (aⁿ^-1 - aⁿ^-2b + aⁿ^-3b² - ... + bⁿ^-1)

Różnica n-tych potęg liczb (dla wszystkich n naturalnych)

aⁿ - bⁿ = (a - b) (aⁿ^-1 + aⁿ^-2b + aⁿ^-3b² + ... + a²bⁿ^-3 + abⁿ^-2 + bⁿ^-1)

Dodaj komentarz

Wzory skróconego mnożenia

Paweł (niezweryfikowany), czwartek, 13/08/2015 - 20:58

We wzorach skróconego mnożenia bardzo fascynuje mnie trójkąt Pascala i wzór z niego wypływający. Wzory skróconego mnożenia są konieczne do nauczenia, ponieważ pojawiają się także przy omawianiu innych działów matematycznych. Zrozumienie ich jest bardzo proste w praktycznych zadaniach. Wzory skróconego mnożenia w bardzo przystępny sposób omówione są także w filmach na kanale YouTube: edudamarek.