Modele ramkowe (2)

Modele ramkowe (2)

Data ostatniej modyfikacji:
2017-07-9

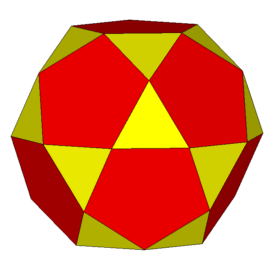
Punktem wyjścia do otrzymania modeli opisanych w tym artykule jest kolejny wielościan archimedesowy – dwudziesto-dwunastościan (rys. 1).

Rys. 1

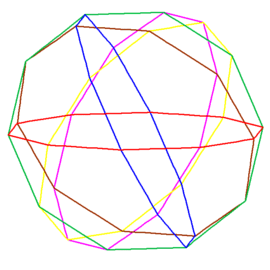
Jego krawędzie możemy pogrupować w 6 dziesięciokątów foremnych (rys. 2, 3).

Rys. 2 Rys. 3

Daje to możliwość wykonania bardzo atrakcyjnego modelu zbudowanego z sześciu dziesięciokątnych ramek (rys. 4).

Rys. 4

Ramki przygotowujemy tak samo, jak w przypadkach opisanej w I części tekstu. Dziesięciokąty przecinają się wzdłuż głównych przekątnych i tak też należy wykonać nacięcia. Pierwszy element ma wszystkie nacięcia od zewnątrz (rys. 5), a drugi ma jedną parę nacięć od wewnątrz (rys. 6).

Rys. 5

Rys. 6

Po ich połączeniu otrzymujemy obiekt przedstawiony na fot. 1.

Fot. 1

Kolejna część ma dwie pary nacięć wewnętrznych. Istotne jest, by były to nacięcia wykonane wzdłuż sąsiednich przekątnych (rys. 7). Tę część dołączamy do poprzednio złożonego fragmentu. Fotografia 2 pokazuje uzyskany rezultat. Zwróćmy uwagę na to, że te trzy elementy zamykają dwa trójkąty – jeden z przodu, a drugi z tyłu.

Rys. 7

Fot. 2

Czwarty element ma trzy pary nacięć od wewnątrz (rys. 8) i powinien być dołączony tak, aby zamknąć kolejne trójkąty poniżej (z przodu) i powyżej (z tyłu) trójkątów otrzymanych wcześniej (fot. 3).

Rys. 8

Fot. 3

Piąta ramka ma już tylko jedną parę nacięć zewnętrznych (rys. 9). Jej dołożenie zamyka dwa pięciokąty. Jeden z nich widoczny jest u dołu po prawej stronie na fot. 4 (drugi znajduje się po przeciwnej stronie modelu).

Rys. 9

Fot. 4

Model kończymy, nakładając ostatni element (rys. 10). Końcowy rezultat pokazuje fot. 5.

Rys. 10

Fot. 5

Bardzo atrakcyjnie wygląda również model jednobarwny (fot. 6).

Fot. 6

Wykonanie tego modelu stanowi pewne wyzwanie. Przygotowanie ramek i odpowiednie ich ponacinanie nie powinno nastręczać większych problemów (kliknięcie tutaj otwiera w nowym oknie stosowny szablon).

Połączenie pierwszych trzech części też nie powinno być kłopotliw, jednak dołożenie kolejnych elementów może sprawić trudność, dlatego należy bardzo uważnie przeanalizować zamieszczone wyżej zdjęcia – zwłaszcza fot. 2 i 3. Nie należy się zniechęcać, bo włożony wysiłek zaowocuje efektowną konstrukcją.

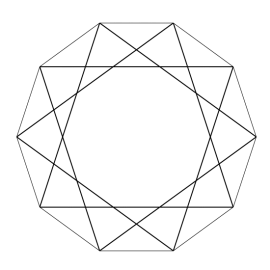
Wprowadźmy teraz małą modyfikację podstawowego elementu – zastąpmy wykorzystany tu wypukły dziesięciokąt foremny przez jego gwiaździstą wersję. Powstaje ona w wyniku poprowadzenia wszystkich przekątnych łączących co trzeci wierzchołek wyjściowego dziesięciokąta foremnego (rys. 11). Ramkę w tym kształcie przedstawia rysunek 12.

Rys. 11 Rys. 12

Jeżeli udało ci się zbudować model z wypukłych dziesięciokątów, to wykonanie modelu z ramek gwiaździstych. nie powinno nastręczać większych trudności. Nacinamy je i łączymy identycznie jak wcześniejsze. Zaczynamy od połączenia ramki ze wszystkimi nacięciami zewnętrznymi (rys. 13) z ramką z jedną parą nacięć wewnętrznych (rys. 14).

Rys. 13 Rys. 14

Następnie dołączamy element z dwoma parami nacięć wewnętrznych (rys. 15), a po nim ten, który ma trzy pary takich nacięć (rys. 16).

Rys. 15 Rys. 16

Przedostatni element ma tylko jedną parę nacięć zewnętrznych (rys. 17), a ostatni ma wszystkie nacięcia od wewnątrz (rys. 18).

Rys. 17 Rys. 18

Efekt końcowy przedstawia fot. 7. Model jest bardzo atrakcyjny i wygląda zupełnie inaczej niż ten powstały z dziesięciokątów wypukłych. Kliknięcie tutaj otwiera w nowym oknie plik ze wszystkimi elementami potrzebnymi do jego wykonania.

Fot. 7

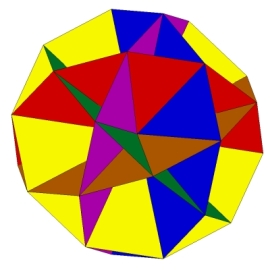
Przyglądając się uważnie otrzymanej konstrukcji, możemy zauważyć, że krawędzie modelu tworzą pentagramy (fot. 8) oraz trójkąty równoboczne (fot. 9). Pentagramów jest 12, a trójkątów 20.

Fot. 8

Fot. 9

Okazuje się, że powstały układ złożony z 6 gwiaździstych dziesięciokątów można na dwa sposoby uzupełnić do niewypukłego wielościanu o foremnych ścianach i przystających wierzchołkach. Powstaną w ten sposób dwa wielościany jednorodne (więcej na temat tej rodziny wielościanów można przeczytać tutaj).

Jeżeli do dziesięciokątnych gwiazd dołączymy pentagramy, to powstanie bryła przedstawiona na fot. 10.