Wszystkie wielościany archimedesowe można otrzymać w wyniku pewnych operacji na wielościanach platońskich.
Siedem z nich powstaje w wyniku odpowiedniego ścinania naroży wielościanów platońskich. Są wśród nich ścięte wersje czworościanu, sześcianu, ośmiościanu, dwunastościanu i dwudziestościanu, a także dwa wielościany zwane sześcio-ośmiościanem i dwudziesto-dwunastościanem. Pierwszy z nich można otrzymać w wyniku ścinania wierzchołków sześcianu lub ośmiościanu, tak by ściąć krawędzie w połowie, drugi powstaje w wyniku analogicznego ścianania wierzchołków dwunastościanu lub dwudziestościanu.
|
czworścian ścięty |
sześcian ścięty |
sześcio-ośmiościan |
ośmiościan ścięty |
|
|
dwunastościan ścięty |
dwudziesto-dwunastościan |
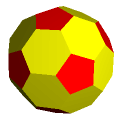 dwudziestościan ścięty |
Otrzymanie pozostałych sześciu wymaga nieco bardziej skomplikowanych operacji, ale ich związek z wielościanami platońskimi jest wyraźnie widoczny.
|
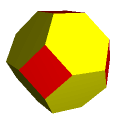
sześcio-ośmiościan rombowy mały |
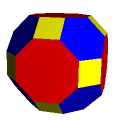
sześcio-ośmiościan rombowy wielki |
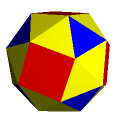
szescio-ośmiościan przycięty |
|
dwudziesto-dwunastościan rombowy mały |
dwudziesto-dwunastościan rombowy wielki |
dwudziesto-dwunastościan przycięty |
Dwa z wielościanów archimedesowych nie posiadają płaszczyzny symetrii (które?), co powoduje, że istnieją w wersji lewo- i prawoskrętnej.
Więcej na temat wzajemnych relacji między wielościanami Archimedesa i Platona można przeczytać w mojej książce W krainie wielościanów. Zrób sobie bryłkę.
Rysunki wielościanów prezentowane na tej stronie zostały wyeksportowane z programu Great Stella.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
