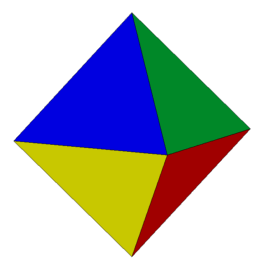
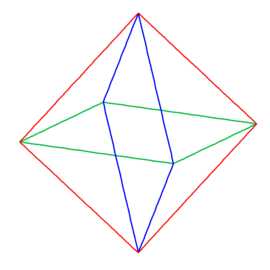
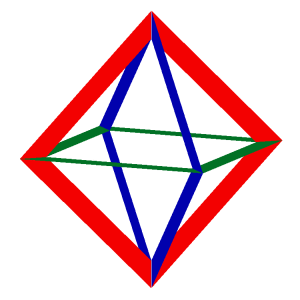
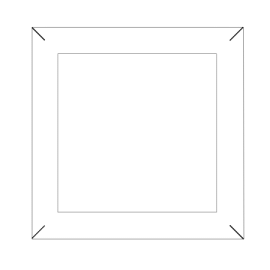
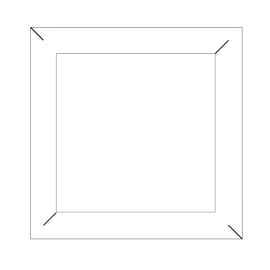
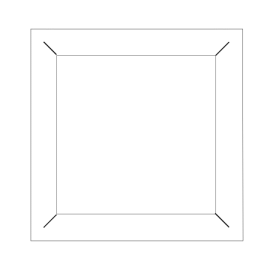
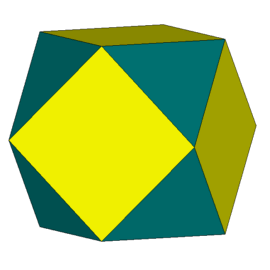
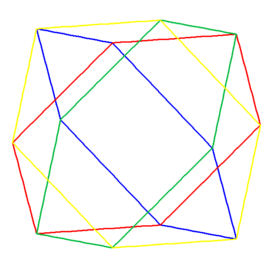
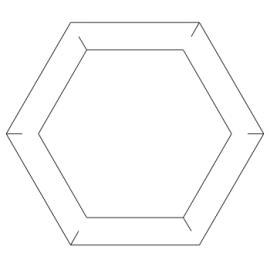
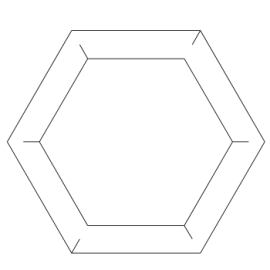
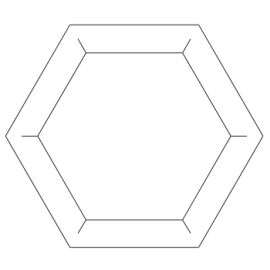
Zacznijmy od spojrzenia na ośmiościan foremny (rys. 1). Chwila obserwacji prowadzi do wniosku, że jego krawędzie można pogrupować po 4 w ten sposób, że otrzymamy 3 kwadraty (rys. 2 i 3).
Rys. 1
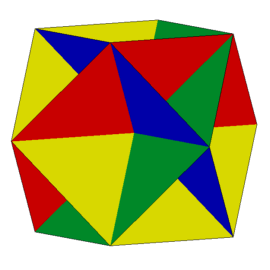
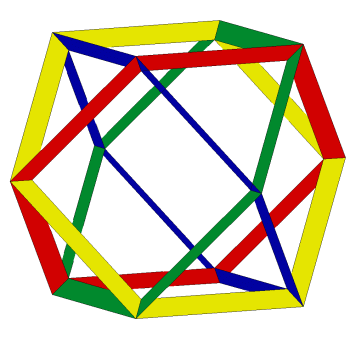
Rys. 2 Rys. 3
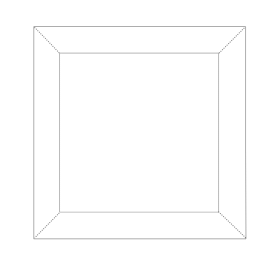
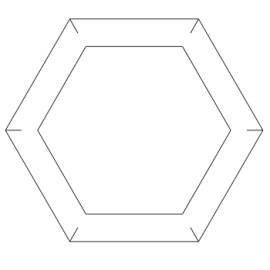
Niewielka modyfikacja powstałych kwadratów prowadzi do bardzo atrakcyjnego modelu przedstawionego na rys. 4.
Rys. 4
Okazuje się, że model ten można z łatwością wykonać bez użycia kleju poprzez połączenie ze sobą trzech odpowiednio ponacinanych ramek. Kwadraty przecinają się wzajemnie wzdłuż przekątnych (rys. 5). Aby można było je połączyć należy je w odpowiedni sposób ponacinać. Pierwszy kwadrat nacinamy tak, jak na rys. 6. Nacięcia zawierają się w przekątnych i prowadzą do połowy szerokości ramki.
Rys. 5 Rys. 6
Uwaga techniczna – aby model dało się dobrze złożyć nie wystarczy tylko wykonać nacięcia. Trzeba wyciąć szczelinę odpowiadającą grubości używanego kartonu. Można to osiągnąć wykonując dwa nacięcia – z lewej i prawej strony narysowanej linii. W ten sposób wycięty zostanie wąski pasek, po wyjęciu którego otrzymamy właściwą szczelinę. Wymaga to pewnej staranności, ale po kilku próbach dojdzie się do właściwej wprawy. Sugeruję, by przed przystąpieniem do wykonywania modelu spróbować wyciąć kilka takich szczelin „na sucho”.
Drugi kwadrat nacinamy tak, jak na rys. 7. Tak przygotowane ramki łączymy ze sobą nakładając jedną na drugą w ten sposób, by „wewnętrzne” nacięcia drugiej ramki spasowały się z jedną parą nacięć pierwszego kwadratu (fot. 1). Przy łączeniu niezbędne jest delikatne wygięcie jednego z kwadratów, ale karton jest na tyle sprężysty, że da się to zrobić bez trwałych odkształceń.
Rys. 7 Fot. 1
Łatwo można dostrzec, że ostatni kwadrat powinien mieć wszystkie nacięcia od wewnątrz (rys. 8).
Rys. 8 Fot. 2
Tak przygotowany element nakładamy na konstrukcję, która jak dotąd była dość wiotka. Dodanie ostatniego elementu stabilizuje położenie wszystkich części składowych i otrzymujemy gotowy model (fot. 2). Można oczywiście wykonać model jednobarwny, który również ma swój urok (fot. 3).
Fot. 3
Szerokość ramki nie może być ani zbyt duża, ani zbyt mała. Elementy takie jak na rys. 9 bardzo trudno jest połączyć bez trwałej deformacji. Im większa jest przestrzeń wewnątrz ramki, tym łatwiej manipulować poszczególnymi elementami. Pamiętać należy jednak też o tym, że w przypadku zbyt wąskiej ramki (rys. 10) istnieje realne niebezpieczeństwo przerwania jej podczas łączenia elementów.
Rys. 9 Rys. 10
Kliknięcie tutaj otwiera w nowym oknie szablon pozwalający wykonać ramkowy model ośmiościanu.
Bazą do wykonania kolejnego modelu będzie archimedesowy sześcio-ośmiościan (rys. 11).
Rys. 11
Jak opisane zostało to w innym miejscu naszego Portalu, jego krawędzie można pogrupować w 4 sześciokąty foremne (rys. 12, 13).
Rys. 12 Rys. 13
Po dokonaniu (analogicznej do wcześniejszej) modyfikacji, otrzymamy piękny model zbudowany z czterech sześciokątnych ramek (rys. 14).
Rys. 14
Przygotowanie tych ramek nie jest istotnie trudniejsze. Podobnie jak wcześniej sześciokąty przecinają się wzdłuż przekątnych (głównych). Tak też należy wykonać nacięcia. Pierwsza ramka ma wszystkie szczeliny od zewnątrz (rys. 15). Druga musi mieć jedną parę szczelin od wewnątrz (rys. 16).
Rys. 15 Rys. 16
Po ich połączeniu otrzymujemy strukturę przedstawioną na fot. 4.
Fot. 4
Kolejny sześciokąt musi być nałożony na dwa już połączone, co oznacza powinien on mieć dwie pary wewnętrznych nacięć (rys. 17). Efekt połączenia trzech ramek prezentuje fot. 5.
Rys. 17 Fot. 5
Ostatni element ma wszystkie nacięcia od wewnątrz (rys. 18). Nakładamy go na trzy pozostałe i otrzymujemy gotowy model (fot. 6).
Rys. 18 Fot. 6
Wykonanie wszystkich sześciokątów w tym samym kolorze daje również ciekawy efekt (fot. 7).
Fot. 7
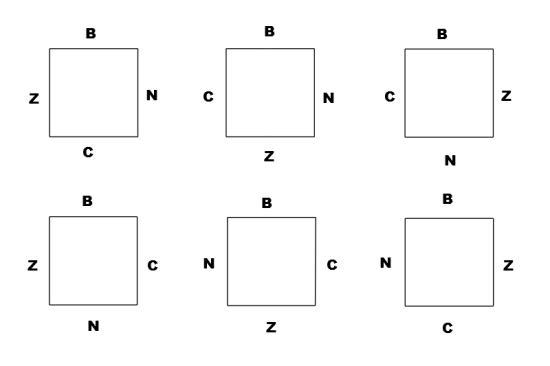
Model kolorowy ma interesujące własności kombinatoryczne. Mając do dyspozycji cztery kolory (powiedzmy, że są to B, N, C, Z) możemy boki kwadratu pomalować tymi kolorami na sześć różnych sposobów (z dokładnością do obrotów) – rys. 19.
Rys. 19
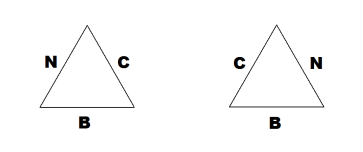
Oglądając model z bliska, możemy przekonać się, że wszystkie możliwe sposoby użycia czterech kolorów do pomalowania boków kwadratu są na nim zrealizowane. Co więcej – z czterech kolorów B, N, C, Z można na cztery sposoby wybrać trzy z nich: BNC, BNZ, BCZ i NCZ. Każdej trójki kolorów można użyć na dwa sposoby do pokolorowania boków trójkąta – rys. 20.
Rys. 20
Otrzymujemy w ten sposób osiem różnych możliwości (z dokładnością do obrotów) pomalowania boków trójkąta. Jak można dostrzec wszystkie one znajdują się na naszym modelu. Dodatkowo – boki trójkątów leżących w płaszczyznach równoległych pomalowane są tą samą trójką kolorów.
Kliknięcie tutaj otwiera w nowym oknie szablon pozwalający wykonać ramkowy sześcio-ośmiościan.
O tym, jak wykonać model ramkowy dzwudiesto-dwunastościanu, piszemy tutaj.
Rysunki i diagramy zostały przygotowane przy użyciu programu Wingeom.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
