W 67, W 68, W 78, W 89, W 91

W67 zwany po angielsku tetrahemixahedron jest najprostszym niewypukłym wielościanem jednorodnym i jedynym mającym nieparzystą liczbę ścian. Jest on ściśle związany z platońskim ośmiościanem (przedstawionym na rys. 1).

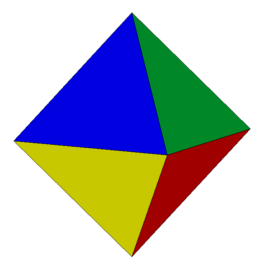
Rys. 1

Krawędzie ośmiościanu foremnego można bowiem pogrupować w trzy grupy po cztery krawędzie w ten sposób, że powstaną trzy wzajemnie przecinające się kwadraty (rys. 2, 3).

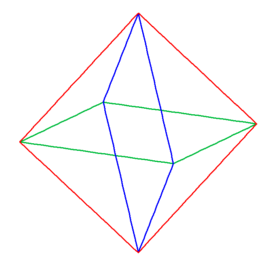
Rys. 2                                                           Rys. 3

W67 powstaje w wyniku uzupełnienia struktury z rys. 3 czterema trójkątami (rys. 4).

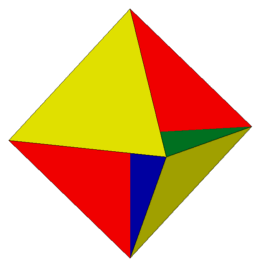
Rys. 4 

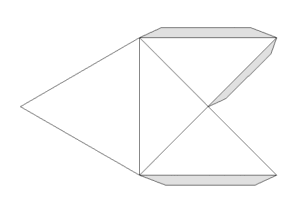
W każdym wierzchołku wielościanu spotykają się dwa trójkąty i dwa kwadraty. Te ostatnie przecinają się, dlatego wierzchołek ma strukturę gwiaździstą. Model tego wielościanu można wykonać, sklejając krawędziami cztery prawidłowe ostrosłupy trójkątne, których ściany boczne są trójkątami prostokątnymi. Siatkę takiego ostrosłupa przedstawia rys. 5 (kliknięcie w obrazek powoduje jego "rozmnożenie" w osobnym oknie).

Rys. 5 

Na pierwszy rzut oka połączenie tych elementów może wydawać się zadaniem trudnym, ale staranne wykonanie poszczególnych ostrosłupów i użycie dobrego kleju pozwala na wykonanie dobrego modelu tego interesującego wielościanu.

Kolejne dwa wielościany - W68 oraz W78 - są ściśle związane z archimedesowym sześcio-ośmiościanem (przedstawionym na rys. 6).

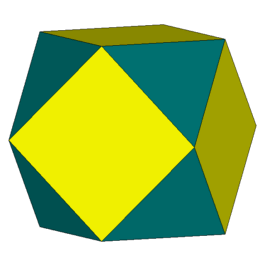
Rys. 6 

Krawędzie sześcio-osmiościanu można bowiem pogrupować po sześć w ten sposób, że wyznaczą one cztery wzajemnie przecinające się sześciokąty foremne (rys. 7, 8).

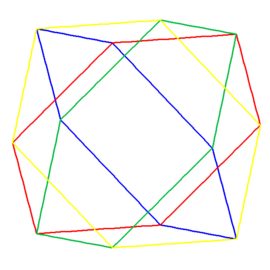
Rys. 7                                                               Rys. 8 

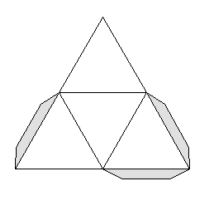
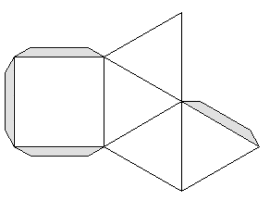
Podobnie jak w poprzednim przypadku, taką strukturę można poprzez dołączenie odpowiednich wielokątów uzupełnić do wielościanu. Tym razem można to zrobić na dwa sposoby - dołączając 8 trójkątów równobocznych lub 6 kwadratów. W wyniku tych operacji powstają odpowiednio W68 (rys. 9) lub W78 (rys. 10).

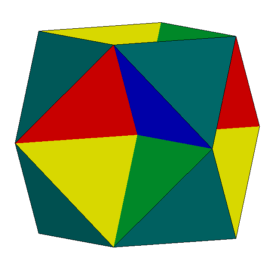
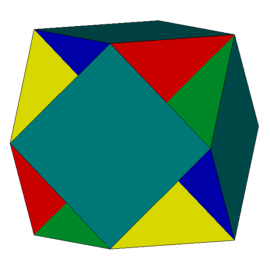
Rys. 9                                                                   Rys. 10

W każdym wierzchołku W68 schodzą się po dwa trójkąty i sześciokąty, a w wierzchołkach W78 - po dwa sześciokąty i kwadraty. Modele obu wielościanów można uzyskać podobnie jak poprzednio, sklejając krawędziami bocznymi odpowiednie ostrosłupy. Sześciokąty foremne z rys. 8 i 9 przecinając się wzajemnie dzielą się na trójkąty równoboczne, wobec tego ściany boczne potrzebnych ostrosłupów są trójkątami równobocznymi. Wykonanie modelu W68 wymaga sklejenia ośmiu czworościanów foremnych, a modelu W78 - sześciu czworokątnych piramid, których ściany są wielokątami foremnymi. Siatki tych ostrosłupów przedstawiają rysunki 11 i 12 (kliknięcie w rysunki otwiera w nowym oknie zduplikowane siatki).

Rys. 11                                                      Rys. 12          

Kolejne dwa wielościany, jakimi się zajmiemy - W89 i W91 - są z kolei (analogicznie jak poprzednie bryły) związane z innym wielościanem archimedesowym - dwudziesto-dwunastościanem (przedstawionym na rys. 13).

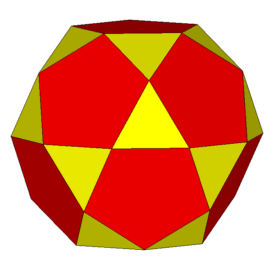
Rys. 13

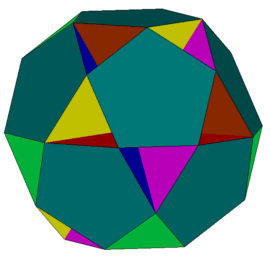
Krawędzie tego ostatniego wyznaczają sześć dziesięciokątów foremnych (rys. 14, 15).

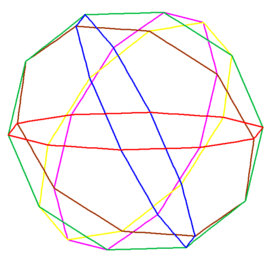
Rys. 14                                                           Rys. 15  

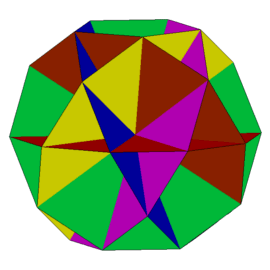
Po uzupełnieniu tej struktury 20 trójkątami równobocznymi otrzymamy wielościan W89 (rys. 16), a po dodaniu do niej 12 pięciokątów foremnych - W91 (rys. 17).

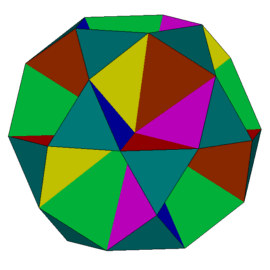
Rys. 16                                                                   Rys. 17

Te wielościany również można otrzymać, sklejając krawędziami odpowiednie ostrosłupy. Ściany boczne tych ostrosłupów są trójkątami równoramiennymi o kącie przy podstawie 72° (bo na takie trójkąty dzielą się przecinające się wzajemnie dziesięciokąty foremne). Do wykonania modelu W89 potrzeba 20 ostrosłupów trójkątnych, których siatka jest na rys. 18, a W91 powstaje po sklejeniu 12 ostrosłupów pięciokątnych, których siatka jest na rys. 19 (kliknięcie w rysunki otwiera w nowym oknie ich zduplikowane powiększenia).

Rys.18                                                            Rys.19     

Nawiasem mówiąc te same ostrosłupy pozwalają zbudować modele dwóch wielościanów Keplera-Poinsota.

Rysunki i diagramy zostały przygotowane przy użyciu programu Wingeom.