W pierwszej części tekstu o modelach szkieletowych z wyciorów opisana została metoda budowania modeli wielościanów, w których wierzchołkach spotykają się cztery krawędzie. W przypadku czworościanu foremnego i sześcianu (a także wielu innych brył) w jednym wierzchołku schodzą się tylko trzy krawędzie. Chcąc zatem wykonać ich modele, należy nieco zmodyfikować opisaną wcześniej metodę.
Spójrzmy na model sześcianu (rys.1). Można zauważyć, że wszystkie jego krawędzie da się podzielić na cztery grupy po 3 krawędzie (rys. 2).

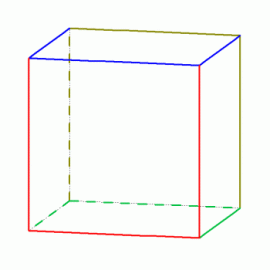
To spostrzeżenie pozwala na bardzo proste wykonanie „wyciorowego” modelu sześcianu. Przygotowujemy 4 druciki. Po zagięciu haczyków na końcach składamy każdy z nich na trzy równe części i formujemy w kształt litery U (fot. 3). Kolejne etapy składania modelu ilustrują zdjęcia 4 i 5. Gotowy model przedstawia fot. 6. Kliknięcie w zdjęcie otwiera w nowym oknie duży obrazek.
Fot. 3 Fot. 4 Fot. 5
Fot. 6
Analogicznie można wykonać model czworościanu foremnego (rys.7, fot. 8).
Rys. 7 Fot. 8
Czworościan ma tylko 6 krawędzi, więc potrzebne będą jedynie 2 wyciory. Oczywiście w przypadku tego modelu wyciory po złożeniu na trzy równe części nie będą formowane w kształt litery U, tylko inaczej – zgodnie z układem krawędzi czworościanu foremnego. Sposób odpowiedniego pogrupowania krawędzi czworościanu i przygotowanie wyciorów pozostawiamy jako zadanie dla Czytelników.
Trzy krawędzie schodzą się w wierzchołkach wielu wielościanów archimedesowych. Przyjrzyjmy się uważniej dwóm z nich.
Rys. 9 przedstawia czworościan ścięty. Podobnie jak we wcześniej opisanych przypadkach, również i tutaj krawędzie można podzielić na grupy po trzy (rys. 10).

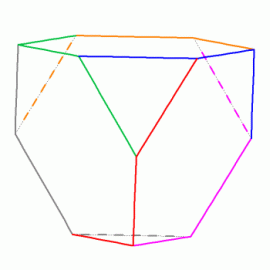
Rys. 9 Rys. 10
Wielościan ten ma 18 krawędzi, więc do wykonania modelu potrzebować będziemy sześciu wyciorów. Nie trzeba jednak aż sześciu kolorów – wystarczą trzy. Gotowy model przedstawia fot. 11. Zauważmy, że środkowa część wyciora odpowiada krawędzi, wzdłuż której stykają się ściany sześciokątne. Pozostałe części to krawędzie styku ściany sześciokątnej i trójkątnej.
Fot. 11
W analogiczny sposób można podzielić krawędzie dwudziestościanu ściętego (rys. 12). Ma on ich aż 90 i po podziale otrzymamy 30 grup. Na rys. 13 wyróżnionych jest 10 takich grup.
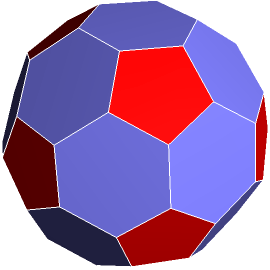
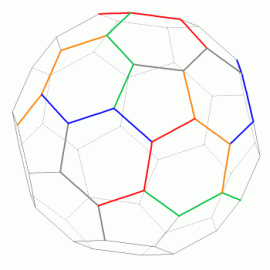
Rys. 12 Rys. 13
Do wykonania modelu potrzeba 30 wyciorów (po 6 w każdym z pięciu kolorów). Podobnie jak poprzednio, środkowa część wyciora odpowiada krawędzi, wzdłuż której stykają się dwa sześciokąty. Skrajne części to krawędzie styku ściany sześciokątnej z pięciokątną. Wykonanie modelu wymaga sporej staranności. Po połączeniu w całość wszystkich elementów model zapewne będzie się deformował. Na szczęście wyciory są elastyczne i z łatwością można wyrównać długości poszczególnych krawędzi, a przede wszystkim właściwie uformować kąty, pod którymi wyciory powinny być pozaginane. Korekt należy dokonywać do czasu, aż otrzymany model zacznie się nam podobać (fot. 14).
Fot. 14
Zachęcamy wszystkich do uważnego przejrzenia katalogu wielościanów archimedesowych i wykonania modeli, które nie zostały opisane w tym tekście. Czekamy na zdjęcia Waszych konstrukcji. Na autorów czekają nagrody.
Rysunki wielościanów w tym tekście zostały przygotowane za pomocą programów Great Stella oraz Wingeom.

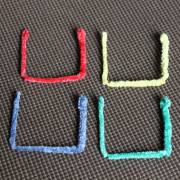










 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
