Piramida Sierpińskiego to fraktal będący przestrzenną wersją trójkąta związanego z nazwiskiem tego wybitnego polskiego matematyka. Punktem wyjścia do tworzenia trójkąta Sierpińskiego jest trójkąt równoboczny, którego każdy z boków dzielimy na dwie równe części. Otrzymane punkty generują podział trójkąta na 4 mniejsze trójkąty równoboczne (rys. 1).


rys. 1 rys. 2
Usuwamy środkowy trójkąt (rys. 2) i do pozostałych trzech stosujemy opisaną wyżej procedurę. Efekty kolejnych etapów przedstawiają rysunki 3-5.


rys. 3 rys. 4

rys. 5
Po czterech krokach "trójkąt" składa się już z 81 małych trójkącików i 40 „dziur". Powierzchnia pozostawionych trójkącików stanowi 81/256 powierzchni wyjściowego trójkąta (dlaczego?). Trójkąt Sierpińskiego powstaje po wykonaniu nieskończonej ilości takich kroków.
Przejdźmy teraz do trzech wymiarów. Przestrzennym odpowiednikiem trójkąta równobocznego jest czworościan foremny. Podzielmy każdą z jego sześciu krawędzi na dwie równe części i poprowadźmy płaszczyzny wyznaczone przez środki krawędzi schodzących się w jednym wierzchołku (rys. 6).
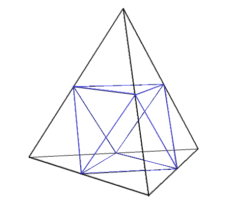

rys. 6 rys. 7
Powstały wewnątrz czworościanu wielościan oczywiście nie jest czworościanem (bo ma 6 wierzchołków), ale każda jego ściana jest trójkątem równobocznym. Policzmy je - na każdej ścianie mamy jeden trójkąt i pod każdym wierzchołkiem czworościanu kolejny. Zatem bryła ta to ośmiościan foremny. Po usunięciu go z czworościanu otrzymamy układ czterech stykających się wierzchołkami czworościanów (rys. 7). To pierwszy krok na drodze do piramidy Sierpińskiego. Każdy z czworościanów jest podobny do wyjściowego w skali ½, zatem objętość całej czwórki to ½ objętości wyjściowego czworościanu (dlaczego?).
Po wykonaniu dwóch kolejnych kroków (rys. 8 i 9) otrzymujemy ażurową konstrukcję złożoną z 64 czworościanów. Ile wynosi stosunek ich objętości do objętości wyjściowego czworościanu?


rys. 8 rys. 9
Zabawę kontynuujemy (rys. 10) i kontynuujemy aż do... nieskończoności.

rys. 10
W efekcie powstaje piramida Sierpińskiego. Ile wynosi jej objętość?
Mimo że w kolejnych przybliżeniach piramidy Sierpińskiego czworościany stykają się tylko wierzchołkami, wykonanie modelu piramidy nie jest niemożliwe. Dobry klej pozwala w miarę trwale połączyć poszczególne elementy. Zaczynamy od przygotowania trzech czworościanów. Po ich sklejeniu ustawiamy je równej i gładkiej powierzchni w ten sposób, by ich podstawy uformowały większy trójkąt i aplikujemy po małej kropli kleju w punktach styczności. Pozostawiamy je na dłuższą chwilę, którą wykorzystujemy na wykonanie kolejnych czworościanów. Gdy klej dobrze zaschnie, trzy czworościany powinny utworzyć w miarę stabilną (choć delikatną) konstrukcję. Po naniesieniu kropli kleju na ich górne wierzchołki ostrożnie stawiamy na nich czwarty czworościan. Zostawiamy całość na dłuższy czas. Pierwsze przybliżenie jest gotowe. W ten sam sposób przygotowujemy jeszcze trzy takie zestawy. Następnego dnia łączymy trzy ażurowe piramidki, a gdy klej dobrze wyschnie, na górze stawiamy czwartą. W ten sposób mamy wykonaną piramidę rzędu 2.
Kliknięcie w poniższy link otwiera w nowym oknie plik z siatkami 16 czworościanów potrzebnych do wykonania opisanego modelu.
Zachęceni sukcesem możemy wykonać jeszcze trzy takie konstrukcje i połączyć je, uzyskując piramidę rzędu 3 (fot. 1, 2 - kliknięcie otwiera w nowym oknie duże zdjęcie). I tak dalej...
fot. 1 fot. 2
W przypadku kłopotów z połączeniem „na styk" można pójść na kompromis i połączyć czworościany za pomocą przezroczystej taśmy klejącej. Natomiast ci, którzy mają trochę zbędnej gotówki, mogą zamówić model wydrukowany na trójwymiarowej drukarce. Odpowiedni plik i efekt jego wydruku można znaleźć tutaj.
Na koniec przyjrzyjmy się jeszcze wyciętym z czworościanu ośmiościanom. One również one tworzą bardzo atrakcyjną fraktalną strukturę (rys. 11).
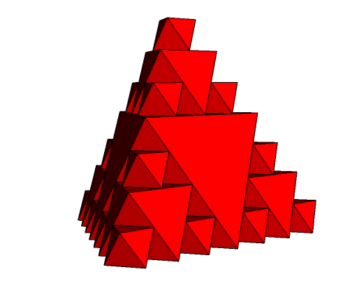
rys. 11
Ponieważ są połączone ścianami, wykonanie modelu (fot. 3) jest zdecydowanie łatwiejsze.

fot. 3
Kliknięcie w poniższe linki otwiera w nowym oknie pliki z siatkami ośmiościanów potrzebnych do wykonania modelu prezentowanego na fot. 3.
16 małych ośmiościanów 4 średnie ośmiościany 1 duży ośmiościan
Rysunki wielościanów zostały wyeksportowane z programu Great Stella. Siatki zostały przygotowane przy użyciu programu Wingeom.






 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
