Inne modele sferyczne

Data ostatniej modyfikacji:
2010-02-10

Jako punkt wyjścia do tworzenia modeli sferycznych mogą posłużyć nie tylko wielościany platońskie, ale również i inne, np. archimedesowe. Jednak ograniczenie się do samych tylko płaszczyzn symetrii tych ostatnich brył nie prowadzi do nowych modeli sferycznych (innych niż te, otrzymane z wielościanów platońskich - dlaczego?). Kiedy wprowadzimy drobne modyfikacje, otrzymamy szereg bardzo interesujących konstrukcji. Jako przykład posłuży nam sześcio-ośmiościan (rys. 1).

Rys. 1

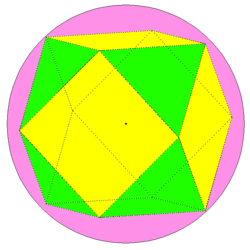
Podobnie jak sześcian i ośmiościan foremny ma on 9 płaszczyzn symetrii. Ich przecięcia z kulą opisaną na tym wielościanie generują ten sam układ trójkątów sferycznych, co w przypadku każdej z tych brył platońskich (rys. 2).

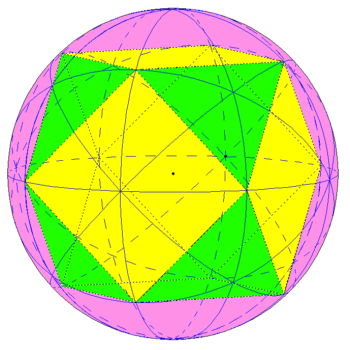
Rys. 2

Możemy jednak ten układ uzupełnić o 4 koła wielkie wyznaczone przez krawędzie sześcio-osmiościanu (rys. 3).

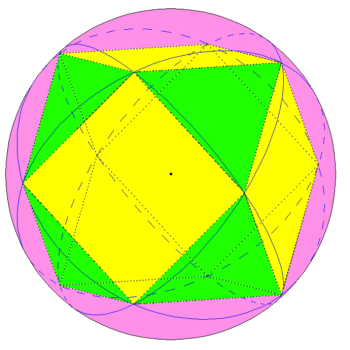
Rys. 3

W ten sposób otrzymamy bardzo interesującą i atrakcyjną strukturę utworzoną przez 13 kół wielkich (rys. 4, 5).

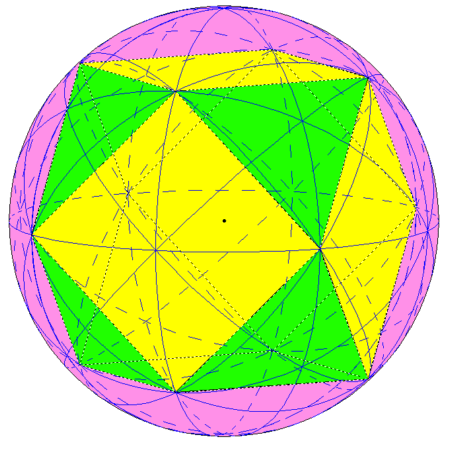
Rys. 4

Rys. 5

Możliwe są też inne modyfikacje. Na ścianach (wszystkich, bądź określonego rodzaju) można narysować ornament (np. przekątne, osie symetrii itp.), który po dokonaniu projekcji na sferę utworzy na niej układ łuków okręgów wielkich. W zależności od wybranego wielościanu i od narysowanego wzoru powstałe w ten sposób łuki uzupełnią się do pełnych okręgów, bądź nie. Za każdym razem powstanie jednak bardzo atrakcyjny model sferyczny. Więcej szczegółów na temat tworzenia takich modeli można znaleźć w książce Magnusa Wenningera Spherical Models.

Poniżej prezentujemy galerię modeli sferycznych wykonanych w opisany wyżej sposób. Kliknięcie w miniaturę otwiera w nowym oknie duże zdjęcie.

Uwaga, konkurs! Odgadnij, jakie wielościany posłużyły za bazy do poszczególnych modeli. Na autorów największej liczby poprawnych odpowiedzi czekają nagrody-niespodzianki.

Fot. 1 Fot. 2 Fot. 3

Fot. 4 Fot. 5 Fot. 6

Fot. 7 Fot. 8

Dodaj komentarz

Odp.

Anonimowy (niezweryfikowany), niedziela, 14/02/2010 - 20:22

Fot. 1 - trójkąt
Fot. 2 - czworokąt
Fot. 3 - trójkąt
Fot. 4 - trójkąt
Fot. 5 - trójkąt
Fot. 6 - pięciokąt
Fot. 7 - trójkąt
Fot. 8 - trójkąt

Odpowiedz

Ejże...

redakcja (niezweryfikowany), piątek, 19/02/2010 - 07:15

W pytaniu wyraźnie chodzi o WIELOŚCIANY!

Odpowiedz

Odpowiedź

tomek20 (niezweryfikowany), czwartek, 08/04/2010 - 21:29

1. sześcio-ośmiościan rombowy wielki
2. ośmiościan ścięty
3. sześcio-ośmiościan
4. dwudziesto-dwunastościan
5. dwudziestościan ścięty
6. dwudziesto-dwunastościan
7. dwunastościan ścięty
8. dwudziestościan ścięty

Odpowiedz

Nie wszystkie są poprawne

redakcja (niezweryfikowany), piątek, 04/06/2010 - 18:44

Wśród odpowiedzi Tomka poprawne są: 2, 3, 4, 6 i 7. W 5 i 8 istotnie można doszukać się pięciokątów i sześciokątów, ale w dwudziestościanie ściętym sześciokąty są foremne, a tu nie. Czekamy na uzupełnienie odpowiedzi.

Odpowiedz

Rozwiązanie konkursu

redakcja (niezweryfikowany), środa, 01/09/2010 - 11:36

Uzupełnienie poprawnych odpowiedzi: 1 to sześcian ścięty, 5 to dwunastościan foremny, a 8 to dwudziesto-dwunastościan. Na upartego można też uznać odpowiedzi: 8 - dwunastościan lub dwudziestościan, 5 - dwudziestościan.