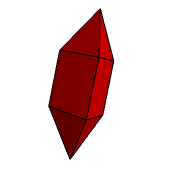
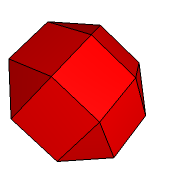
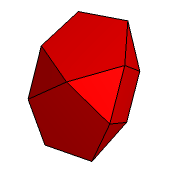
Każdy z łatwością może podać przykłady wielościanów wypukłych o foremnych ścianach. Takimi są oczywiście wszystkie wielościany platońskie i archimedesowe, a także prawidłowe graniastosłupy i antygraniastosłupy o odpowiednio dobranej wysokości (tak aby wszystkie krawędzie miały tę samą długość). Jeszcze innymi przykładami (które do tej pory nie pojawiły sie w Galerii) są prawidłowe ostrosłupy czworokątny i pięciokątny o foremnych ścianach bocznych (ryc. 1, 2). Jeśli ostrosłup pięciokątny odetniemy od dwudziestościanu foremnego, to co pozostanie też będzie dobrym przykładem (ryc. 3).
|
Ryc. 1 |
Ryc. 2 |
Ryc. 3 |
Stosując operacje odcinania bądź doklejania do innych znanych brył łatwo można znaleźć więcej przykładów takich wielościanów. Opisz, jak powstały bryły z ryc. 4-6.
|
Ryc. 4 |
Ryc. 5 |
Ryc. 6 |
Dokładne określenie liczby wszystkich wielościanów tego typu nie jest proste. Na początku lat 60. wieku XX Norman Johnson wykazał, że ściany takich wielościanów mogą być tylko trójkątami, kwadratami, pięciokątami, sześciokątami, ośmiokątami lub dziesięciokątami foremnymi oraz że istnieje skończona liczba takich wielościanów. W 1966 roku opublikował zaś listę 92 wypukłych wielościanów o foremnych ścianach (dziś są one nazywane wielościanami Johnsona). Postawił również hipotezę, że lista ta jest kompletna, nie potrafił jednak uzasadnić tego faktu. Rok później Rosjanin Wiktor Załgaller wykazał, że lista Johnsona zawiera wszystkie wypukłe wielościany o foremnych ścianach, nie będące wypukłymi wielościanami jednorodnymi.
Siedemnaście z tych brył to wielościany proste - tzn. takie, których nie można podzielić na mniejsze wielościany o foremnych ścianach. Kilka przykładów takich wielościanów przedstawiono na ryc. 7-9. Pozostałe 75 wielościanów można otrzymać w wyniku sklejania ścianami wielościanów prostych lub odcinania fragmentów tych wielościanów.
|
Ryc. 7 |
Ryc. 8 |
Ryc. 9 |
Wszystkie półforemne graniastosłupy i antygraniastosłupy są proste (z wyjątkiem antygraniastosłupa trójkątnego, czyli ośmiościanu foremnego, który powstaje ze sklejenia podstawami dwóch ostrosłupów kwadratowych). Wśród brył platońskich wielościany proste to czworościan, sześcian i dwunastościan. Zachęcam do samodzielnego znalezienia pozostałych wielościanów prostych wśród brył archimedesowych oraz wśród pozostałych wielościanów Johnsona.
Z jakich brył prostych składają się wielościany Johnsona, które same proste nie są? Czy zawsze można je skleić z brył prostych tylko na jeden sposób? A które powstają z odcięcia części wielościanów prostych?
Wizerunki wielościanów zostały wyeksportowane z programu Great Stella.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Błąd
Na ryc. 5 jest błąd, ponieważ kopuły czworokątnej nie da się "zbudować" z innych wielościanów.
Można sklejać lub odcinać
To prawda, że kopuły czworokątnej nie da się rozciąć na wielościany o foremnych ścianach, ale przecież można ją otrzymać poprzez odcięcie fragmentu archimedesowgo sześcio-ośmiościanu rombowego małego. Można to porównać z bryłą z rys. 3, która jest rezultatem odcięcia czegoś od dwudziestościanu.
Jest też inny sposób
Jest też inny sposób. Potrzebne są 3 sześciany i 2 graniastosłupy trójkątne o foremnych ścianach. Trzeba nieco poodcinać ściany (nie będą foremne).
Niedobry sposób
Pomysł Polaka nie jest dobry. Kopuła czworokątna jest za niska na to. Jeżeli się ją potnie, to środkowa bryła nie będzie sześcianem, a z pozostałych części też nie wyjdą sześciany.