Zad. 1. Pan Paweł należy do Klubu Turystycznego "Wiewiórka". Jest to grupa licząca 40 osób, wśród których 25 osób uprawia turystykę pieszą, 12 - turystykę rowerową i 15 - turystykę motocyklową. Ile osób uprawia jednocześnie turystykę rowerową i motocyklową, jeżeli wiadomo, że tylko pan Paweł i jego dwaj koledzy uprawiają wszystkie rodzaje turystyki, 2 osoby uprawiają tylko turystykę pieszą i rowerową, a 1 osoba tylko turystykę pieszą i motocyklową?
Zad. 2. W zbiorze dodatnich liczb całkowitych określamy operacje: {a} = a4 i [a|b] = a+b. Ile wynosi wartość wyrażenia {[{2}|{2}]}?
Zad. 3. Ile liczb naturalnych n spełnia nierówność [tex]99< \sqrt{n+100}<101[/tex]?
W styczniu punkty zdobyli:
- 3 – Eliza Banaszkiewicz SP Strzelce, Natalia Czurejno SP Wykroty, Anna Frankowska SP 139 Warszawa, Antoni Grębowiec SP 44 Wrocław, Aleksander Masztalski SP 3 Mikołów, Szymon Michalik SP 3 Przymierza Rodzin Warszawa, Ewa Nowakowska SP Strzelce, Karolina Piątkowska SP 16 Wrocław, Alicja Picińska SP 64 Wrocław, Aleksandra Pniaczek SP 50 Wrocław, Barbara Podoba SP 2 Tomaszów Lubelski, Gabriela Pułecka SP 2 Brzeg Dolny, Wojciech Radomyski SP Pilawa, Yaraslau Sialiuk SP 82 Wrocław, Jan Węgrzyn SP 44 Wrocław, Ignacy Włodarski SP 36 Wrocław;
- 2 – Julia Strzelecka SP 50 Wrocław, Krzysztof Pajek SP 50 Wrocław;
- 1 – Zygmunt Pielak SP Celestynów.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
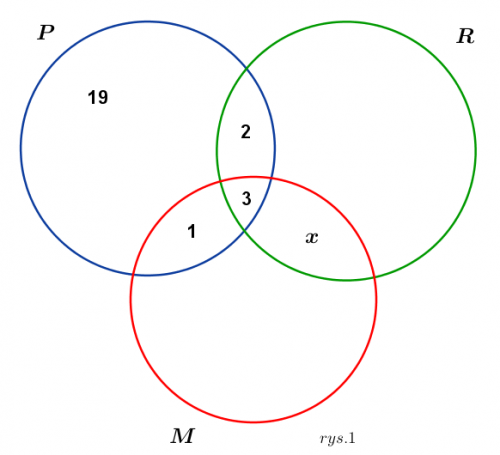
Zad. 1. Niech P, R, M będą odpowiednio zbiorami osób uprawiających turystykę pieszą, rowerową i motocyklową, a x – liczbą osób uprawiających jednocześnie turystykę rowerową i motocyklową. Na podstawie treści zadania wiemy, że 3 osoby uprawiają wszystkie rodzaje turystyki, 2 osoby uprawiają tylko turystykę pieszą i rowerową, a 1 osoba tylko turystykę pieszą i motocyklową. Stąd 25–(3+2+1) = 19 osób uprawia tylko turystykę pieszą (rys. 1). Zatem 40–19 = 21 osób uprawia turystykę rowerową lub motocyklową. Z drugiej strony 12+15 = 27, więc 6 osób uprawia jednocześnie turystykę rowerową i motocyklową, w tym 3 osoby uprawiają wszystkie rodzaje turystyki (rys. 2). Ostatecznie 6–3 = 3 osoby uprawiają jednocześnie turystykę rowerową i motocyklową.

Zad. 2. {[{2}|{2}]} = {[24|24]} = {24+24} = {2.24} = {25} = (25)4 = 220.
Zad. 3. Nierówność daną w zadaniu możemy zapisać jako 992< n+100 <1012. Zachodzą zatem nierówności: 992–100 < n i n < 1012–100. Nierówność podaną w zadaniu spełnia (1012–100)–(992–100)–1 = (1012–992)–1 = (101–99)(101+99)–1 = 400–1 = 399 liczb naturalnych.