Zad. 1. Przez jaki czas w ciągu doby na wyświetlaczu zegarka elektronicznego pokazującego czas w formacie 24-godzinnym (HH:MM) widoczna jest dokładnie jedna cyfra 8?
Zad. 2. Marek i Andrzej porównali swoje oszczędności, po czym Marek stwierdził: Razem mamy 500 złotych, ale gdyby moje oszczędności wzrosły o 20%, a twoje zmalały o 20%, mielibyśmy po równo pieniędzy. Jaką część oszczędności Andrzeja stanowi kwota posiadana przez Marka?
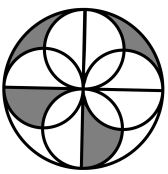
Zad. 3. Promień dużego koła ma długość 2 cm, a długości promieni czterech mniejszych kół są dwa razy mniejsze. Wspólny punkt czterech mniejszych kół pokrywa się ze środkiem dużego koła. Oblicz pole zacieniowanej części.
W marcu punkty zdobyli:
• 3 pkt. – Igor Wojtasik SP 11 Jelenia Góra, Laura Stefanowska G Legnica, Bartosz Nodzak SP 152 Łódź, Joanna Galik SP 5 Wrocław, Wojciech Szwarczyński PSP Kowalowa, Piotr Zug SP 1 Borki Wielkie, Maciej Michoń MZS Strzyżowa, Jerzy Wąsiewicz Publiczna Katolicka SP Magdalenka, Oliwer Rum PG 1 Głogówek, Kosma Kasprzak G 58 Poznań, Gabriela Pietras PSP Leszczyna, Marta Sibielec G 48 Wrocław, Agata Lefler ZSS Wołów, Tomasz Lefler ZSS Wołów, Jakub Dubiel SP 5 Wrocław, Patrycja Zakrzewska G Tuchola i Stanisław Schlaffke G 1 Swarzędz.
• 2 pkt. – Fabian Mikuszewski SP 2 Strzyżow, Maksymilian Szczepaniak SP Siechnice, Kacper Woszczek PSP Mieroszów i Wiktoria Cymerman G-Europejskie Zgorzelec.
• 1 pkt. – Filip Czarnik MZS Strzyżów, Hubert Bączyk G 1 Swarzędz i Krzysztof Jopek.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. W ciągu godziny na minutowej części wyświetlacza cyfra 8 widnieje przez minutę 6 razy (:08, :18, :28, :38, :48, :58). Ponadto w ciągu dwóch godzin przez 54 minuty wyświetlana jest jedna cyfra 8 w części godzinowej wyświetlacza (08: oraz 18:). Podsumowując, w ciągu doby dokładnie jedna cyfra 8 jest widoczna przez 2·56 + 22· = 240 minut = 4 godziny.
Zad. 2. Do rozwiązania zadania nie trzeba wiedziec, ile pieniędzy mają chłopcy. Mamy bowiem 1,2M=0,8A, czyli 3/2M = A, zatem M = 2/3 A, więc kwota posiedana przez Marka stanowi 2/3 oszczędności Andrzeja.
Zad. 3. Sposób I. Wykażemy, że zachodzi równość pól f1 i f2 (patrz rysunek). Oznaczmy promień dużego koła OA jako 2r, wtedy promień małego koła to r. Pole ćwiartki koła wynosi 1/4π(2r)² = 2·1/2πr² – f1+ f2. Stąd f₁ = 2·1/2πr² – 1/4·4πr² + f₂, czyli f1 = f2. Pole zacieniowanej części figury składa się z czterech elementów i jest równe ¼ pola koła o promieniu 2, czyli 1/4π(2)² = π.
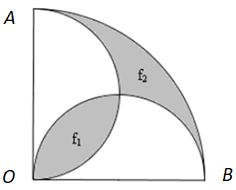
II sposób. Szukane pole zacieniowanej części jest równe polu zaznaczonemu kolorem pomarańczowym na poniższym rysunku, czyli Pf = 1/2π·2² –π·1² = π.
