Zad. 1. Smerf Obżartuch zjada na śniadanie trzy jednakowe miseczki owsianki, jedną po drugiej. Kiedy zjadł 3/7 całej owsianki przewidzianej na śniadanie, to jaki zjadł ułamek owsianki z drugiej miseczki?
Zad. 2. W pewnej szkole piąta część uczniów ma niebieskie oczy, ale tylko dziesiąta część uczniów leworęcznych oraz czwarta część uczniów praworęcznych z tej szkoły ma niebieskie oczy. Jaki jest ułamek uczniów leworęcznych w szkole?
Zad. 3. Rysunek przedstawia romb PQRS i trójkąt równoramienny PQT (gdzie |PT|=|QT|). Jaką miarę ma kąt SQT?
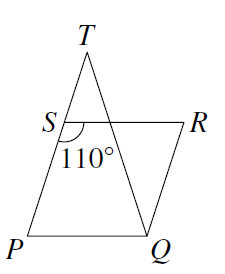
W listopadzie punkty zdobyli:
- 3 – Wiktor Gatner SP 24 Wrocław, Zuzanna Garbecka SP 2 Szczytno, Anita Głowacz SP Popielów, Paweł Jarzyński SP 13 Zielona Góra, Amelia Łakomiec SP 50 Wrocław, Oksana Manowska SP 2 w Szczytnie, Alicja Picińska 64 Wrocław, Mateusz Plaminiak SP 39 Wrocław, Stanisław Solski SP 13 Zielona Góra, Natasza Sosnal SP 16 Wrocław, Yaraslau Sialiuk SP 82 Wrocław, Filip Staszkiewicz SP 50 Wrocław, Lena Szkirpan SP 50 Wrocław, Emilia Wahl SP Popielów, Marcin Węgrzyn SP 44 Wrocław, Ignacy Włodarski SP 36 Wrocław, Michał Wróblewski SP Bielkówko;
- 2 – Adam Gajdzis SP 107 Wrocław, Claudia Jończyk SP Jedlnia Letnisko Darya Karnitskaya SP 107 Wrocław, Adam Kosarzycki SP 16 Wrocław, Joanna Kubik SP 3 Oleśnica, Hanna Łukasik SP 50 Wrocław, Maksymilian Mączka SP STO Warszawa, Igor Pac SP 2 Szczytno, Wiktor Szwarczyński SP Szkoła w chmurze Poznań, Adam Teleśnicki SP 50 Wrocław, Leon Wilczyński SP 113 Wrocław, Kacper Ziółek SP 2 Szczytno, Dawid Zysk SP 19 Legnica;
- 1 – Szczepan Buczkowski SP 2 Ożarów Mazowiecki, Jakub Derewecki SP 50 Wrocław, Hanna Kulpińska SP 50 Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Obżartuch zjadł 3/7 całej owsianki, czyli 3/7.3 = 9/7 = 12/7 miseczki, co znaczy że zjadł jedną całą miseczkę owsianki i 2/7 z drugiej.
Zad. 2. Niech p i l oznaczają liczby uczniów prawo- i leworęcznych w szkole. Z warunków zadania mamy (p+l)/5 = p/4+l/10. Mnożąc obie strony równania przez 20, otrzymujemy 4p+4l = 5p+2l, skąd p=2l, czyli wszystkich uczniów było 3l, z czego 1/3 stanowili leworęczni.
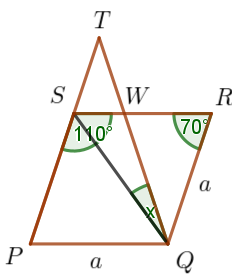
Zad. 3. Kąt ostry rombu ma 180°–110° = 70°, a z równoramienności trójkąta PQT mamy
|∡SPQ|=|∡PQT|=70°. Z własności rombu |SP|=|PQ|, więc trójkąt SPQ jest równoramienny z kątem PQS przy podstawie mającym (180°–70°):2 = 55°. Stąd x =70°–55°=15°.
