Zad. 1. Lena i Nadia ozdabiają choinkę, ciesząc się świąteczną atmosferą. Nagle ich łańcuch z koralików pęka, a koraliki rozsypują się po całym pokoju. Dziewczynki zaczynają poszukiwania – znajdują jedną trzecią koralików na podłodze pod choinką, jedną czwartą pod szafką, a kolejną piątą część za oparciem kanapy. Na sznurku pozostała jeszcze szósta część koralików, ale sześciu koralików wciąż brakuje. Ile koralików było na łańcuchu na początku?
Zad. 2. Świętemu Mikołajowi pomaga 320 elfów. Spośród nich ¾ ma żony, które również wspierają ich w pracy. Dodatkowo ¾ żonatych elfów ma przynajmniej jedno dziecko, a ¾ elfów, którzy są ojcami, ma więcej niż jedno dziecko. Wszyscy: elfy, ich żony oraz dzieci wspólnie pomagają Mikołajowi w przygotowywaniu prezentów. Oblicz, ilu co najmniej pomocników ma Mikołaj.
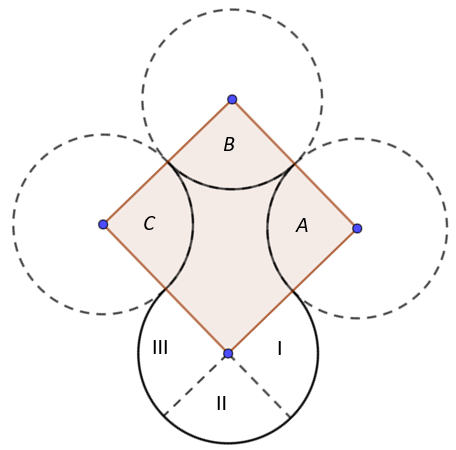
Zad. 3. Rysunek wazonu został utworzony z trzech ćwiartek okręgów oraz jednego fragmentu, który stanowi trzy czwarte okręgu. Promienie wszystkich okręgów wynoszą 10 cm. Oblicz pole tej figury.
Zad. 1. Oznaczmy przez x początkową liczbę koralików. Z treści zadania wiemy, że x/3 + x/4 + x/5 + x/6 + 6 = x, skąd otrzymujemy x=120.
Zad. 2. Obliczmy, ilu elfów ma żony: 3/4·320 = 240. Teraz obliczmy, ilu żonatych elfów ma przynajmniej jedno dziecko: 3/4·240=180. Następnie obliczmy, ilu elfów ma więcej niż jedno dziecko: 3/4·180=135. Liczba elfów, którzy mają dokładnie jedno dziecko, wynosi 180−135=45. Wszyscy pomocnicy Mikołaja to: 320 elfów, 240 żon, 45 dzieci (elfów z jednym dzieckiem) i co najmniej 2⋅135 dzieci (elfów z więcej niż jednym dzieckiem). Ostatecznie Mikołaj ma co najmniej 320+240+45+270=875 pomocników.
Zad. 3. Zaznaczmy środki i narysujmy okręgi. Zauważmy, że gdy przesuniemy ćwiartki I, II i III w miejsca A, B i C, otrzymamy kwadrat o boku 20 cm. Zatem pole wazonu wynosi 20.20 = 400 cm2.
