Zad. 1. Jeśli renifery będą ciągnęły sanie Mikołaja ze średnią prędkością 90 km/h, dotrze on do Wrocławia godzinę przed pojawieniem się pierwszej gwiazdki. Jeśli jednak będą jechały ze średnią prędkością 60 km/h, Mikołaj przybędzie godzinę po jej pojawieniu się. Z jaką średnią prędkością powinny biec renifery, aby Mikołaj dotarł do naszego miasta dokładnie w momencie, gdy zabłyśnie pierwsza gwiazdka?
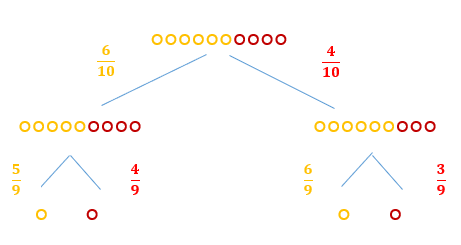
Zad. 2. W pudełku jest sześć bombek złotych i cztery czerwone. Paweł wyjmuje na chybił trafił jedną bombkę po drugiej. Jakie jest prawdopodobieństwo, że druga bombka, którą wyjmie, będzie czerwona?
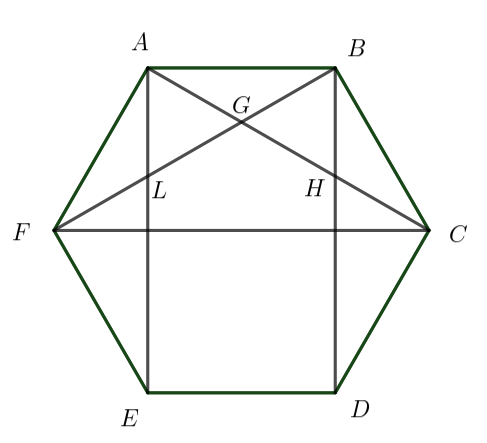
Zad. 3. Lena i Nadia przygotowują ozdoby choinkowe ze słomianych ramek w kształcie sześciokątów foremnych. Kolorowymi włóczkami łączą co drugi wierzchołek. Wówczas wewnątrz ramki powstaje mniejszy włóczkowy sześciokąt. Lena twierdzi, że on również jest foremny, ale Nadia ma co do tego wątpliwości. Która z dziewczynek ma rację? Uzasadnij odpowiedź.
W grudniu punkty zdobyli:
- 3 – Zuzanna Czapiewska ZSB Słupsk, Stanisław Pająk LO Żary;
- 2,5 – Artur Bumażnik ZSE Jelenia Góra, Emilia Cichowska II LO Lubin, Liliana Ottlik III LO Wrocław, Paweł Prasal III LO Leszno, Gabriela Pułecka V LO Wrocław, Mieszko Ratajczak II LO Głogów, Cezary Rębiś ZSE Radom, Oliwier Roszkowski X LO Wrocław, Miłosz Zakrzewski LO Tuchola;
- 2 – Mikołaj Idzikowski I LO Ostrzeszów, Jagoda Janiś LO Góra, Anna Niżałowska LO Góra, Joanna Nowakowska LO Aslan Głogów, Igor Sudyka V LO Kraków, Paulina Wójcik LO Dobrzeń Wielki;
- 1 – Hubert Kosmala II LO Oleśnica.
Pozostali uczestnicy otrzymali poniżej 1 punktu
Zad. 1. Oznaczmy przez s - drogę jaką ma pokonać Mikołaj, v - prędkość z jaką powinny biec renifery, t - czas potrzebny na przebycie drogi s. Drogę obliczamy, korzystając ze wzoru s=vt. Z treści zadania wynika, że s = 90·(t–1) = 60·(t+1), skąd t=5. Zatem 5v = 90·4, skąd
v = 72 km/h.
Zad. 2. Obliczymy prawdopodobieństwo za pomocą drzewa, korzystając z reguły mnożenia i dodawania. Paweł za pierwszym razem może wyjąć bombkę złotą lub czerwoną. Prawdopodobieństwo wyjęcia bombki złotej wynosi 6/10, a czerwonej - 4/10. Za drugim razem analizujemy zdarzenie, że Paweł wyjmie bombkę czerwoną. Jeśli za pierwszym razem wylosował bombkę złotą, w pudełku zostaną 4 bombki czerwone i 5 złotych. Prawdopodobieństwo wylosowania bombki czerwonej w drugim kroku wynosi 4/9. Jeśli za pierwszym razem wyjął bombkę czerwoną, w pudełku zostają 3 bombki czerwone i 6 złotych. Prawdopodobieństwo wylosowania bombki czerwonej w drugim kroku wynosi 3/9. Obliczamy całkowite prawdopodobieństwo zdarzenia, że druga bombka będzie czerwona: P(A) = 6/10·4/9 + 4/10·3/9 = 2/5.
Zad. 3. Zewnętrzny sześciokąt jest foremny, zatem |AB| = |BC| i |∡ABC| = 120°. Trójkąt ABC jest równoramienny, zatem |∡BAC| = |∡BCA| = (180–120)/2 = 30°. Podobnie Trójkąt FAB jest równoramienny i |∡ABF| = 30°, więc kąty LGH i AGB przystają jako wierzchołkowe i |∡LGH| = |∡AGB| = 180–2∙30 = 120°, czyli kąt przy wierzchołku G w wewnętrznym sześciokącie ma 120°. W podobny sposób stwierdzamy, że każdy kąt wewnętrznego sześciokąta ma miarę 120°, jednak sześciokąt równokątny nie musi być foremny (dlaczego?). Musimy wykazać, że sąsiednie boki wewnętrznego sześciokąta mają taką samą długość. W tym celu zastosujemy cechę przystawania trójkątów kbk, na podstawie której stwierdzimy, że trójkąty GLA i GHB są przystające. Zachodzi bowiem |∡GBH| = |∡ABC|–|∡ABG|–|∡DBC| = 120°–2∙30 = 60°. Podobnie |∡LAG| = 60°, skąd |∡LAG| = |∡GBH|. Ponadto trójkąt GAB jest równoramienny, gdyż |∡BAC| = |∡ABF| = 30°, skąd |GA| = |GB|. Zachodzi też |∡LGA| = |∡HGB|, bo są to kąty wierzchołkowe. Ponieważ wszystkie części przystających trójkątów przystają, otrzymujemy |LG| = |HG|, cnd.