Kwadrat

Definicja:
Kwadrat to wielokąt płaski, który jest czworokątem foremnym, tzn. takim, który ma przystające wszystkie boki i wszystkie kąty wewnętrzne.

Oznaczenie:
[tex] \fbox{$\color{white}^{\;^{\;}}$}[/tex]ABCD (czytaj: kwadrat o wierzchołkach A, B, C, D)

Pochodzenie nazwy:
Polska nazwa kwadrat pochodzi od łacińskiego słowa quadratus, co znaczy czworoboczny.

Elementy składowe kwadratu:

• punkty A, B, C i D to wierzchołki kwadratu,
• odcinki AB, BC, CD i DA to boki kwadratu,
• odcinki AC i BD to przekątne kwadratu,
• łamana zamknięta ABCDA to brzeg kwadratu.

Konstrukcja:

sposób 1	sposób 2
Kroki:	Kroki:

Definicje alternatywne:

• prostokąt o bokach równej długości,
• prostokąt o prostopadłych przekątnych,
• prostokąt, którego przekątne połowią kąty wewnętrzne,
• prostokąt, w który można wpisać okrąg,
• prostokąt symetryczny względem przekątnej,
• romb o przystających kątach wewnętrznych,
• romb o przekątnych równej długości,
• romb, na którym można opisać okrąg.

Przykłady:

• kwadrat wpisany w okrąg,
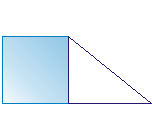
• kwadrat zbudowany na boku trójkąta,
• kwadrat w układzie współrzędnych zadany nierównością |x|+|y|$\leq$1,
• kwadrat w układzie współrzędnych zadany nierównością max(|x|, |y|)$\leq$1.

Kontrprzykłady:

• prostokąt - kąty proste, ale boki nie są równej długości,
• romb - boki przystające, ale kąty nie,
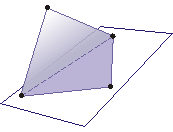
• kwadrat zwichrowany - boki równej długości i kąty proste, ale wierzchołki nie leżą w jednej płaszczyźnie,
• sześcian - nie jest wielokątem,
• kwadrat niemożliwy - nie jest realizowalny geometrycznie.

Własności:

• kwadrat o jednostkowym boku stanowi standardową jednostkę pola,
• na każdym kwadracie można opisać okrąg,
• w każdy kwadrat można wpisać okrąg,
• punkt przecięcia przekątnych jest środkiem okręgu opisanego na i wpisanego w kwadrat,
• kwadraty szczelnie wypełniają płaszczyznę (tworzą parkietaż),
• cecha przystawania kwadratów: równość boków,
• wszystkie kwadraty są podobne,
• kwadrat można rozciąć na mniejsze kwadraciki, z których każdy jest inny,
• dwa kwadraty można rozciąć na części, z których można złożyć jeden kwadrat,
• istnieje tylko jeden wielościan foremny o kwadratowych ścianach (sześcian).

Związki miarowe:
W kwadracie o boku długości a mamy:

• pole P = a²
• obwód O = 4a
• przekątna d = $a\sqrt{2}$
• kąt wewnętrzny ma miarę 90°
• suma kątów wewnętrznych wynosi 360°
• suma kątów zewnętrznych wynosi 360°
• promień okręgu opisanego R = $\frac{a\sqrt{2}}{2}$
• promień okręgu wpisanego r = $\frac{a}{2}$

Historia:

• Kwadrat odgrywał dużą rolę już w starożytnym Egipcie, o czym świadczą zabytki architektury, np. piramidy o podstawie kwadratowej (3 tys. lat p.n.e.). Egipcjanie przyjmowali za jednostkę pola jednostkowy kwadrat. Potrafili obliczyć pole dowolnego kwadratu.
• Widoczna na zdjęciu gliniana tabliczka pochodząca z Babilonu z II w. p.n.e. przedstawia kwadrat z przekątnymi. Z zapisu na tabliczce można odczytać stosunek długości przekątnej kwadratu do jego boku (zapisany w systemie 60-kowym). Różni się od rzeczywistej wartości $\sqrt{2}$ dopiero na szóstym miejscu po przecinku.

• Pitagoras i jego uczniowie odkryli w V w. p.n.e. (i ściśle udowodnili), że dwa kwadraty można rozciąć na części, z których zbudować nowy kwadrat.
• Według Proklosa Pitagorejczycy pokazali również, że płaszczyznę można pokryć jednakowymi kwadratami.
• Euklides ok. 300 r. p.n.e. w swoim najsłynniejszym dziele Elementy podaje, że kwadrat to ta z figur czworobocznych, która jest zarówno równoboczna jak i posiada wszystkie kąty proste. Opisuje również konstrukcję kwadratu, którego dany bok zawiera się w danej prostej.
• Teodoros z Cyreny (2 poł. V wieku) potrafił dowieść niewspółmierności boku i przekątnej dla kwadratów o polach wyrażających się liczbami całkowitymi nie przekraczającymi 17. Zaś jego uczeń Teajtet pozbył się tego ograniczenia.

• kwadrat liczby
• kwadrat logiczny
• kwadrat łaciński
• kwadrat magiczny

• H. Coxeter, S.Greitzer, Geometry Revisited, MAA, Washington, DC, 1967.
• Euklides, Elementy, http://aleph0.clarku.edu/~djoyce/java/elements/elements.html
• J. Mioduszewski, Ciągłość szkice z historii matematyki, WSiP, Warszawa 1996.
• Tablice matematyczne pod red. W. Mizerskiego, Adamantan, Warszawa 2002.
• Ian Stewart, Histerie matematyczne Gry i zabawy z matematyką, Prószyński i S-ka, Warszawa 2007.
• W. Więsław, Matematyka i jej historia, Nowik, Opole 1997.