Definicja
Kąt to każdy z dwóch obszarów płaszczyzny wyznaczonych przez dwie półproste o wspólnym początku, wraz z tymi półprostymi.

Elementy składowe kąta:
- punkt O to wierzchołek kąta,
- półproste OA i OB to ramiona kąta,
- ramiona kąta tworzą jego brzeg,
- otwarty obszar płaszczyzny wycięty przez ramiona to wnętrze kąta.
Oznaczenia
Stosuje się różne oznaczenia:
- mała, pojedyncza litera alfabetu greckiego, np. $\angle$α,
- duża litera alfabetu łacińskiego oznaczająca punkt w wierzchołku kąta, np. $\angle A$
- trzy duże litery alfabetu łacińskiego oznaczające kolejno punkt na 1. ramieniu, wierzchołek i punkt na 2. ramieniu kąta, np. $\angle AOB$.
Napis $\angle AOB$ jest niejednoznaczny. Może oznaczać każdy z dwóch kątów, które zostały utworzone przez półproste OA i OB.
Definicje alternatywne
- Nieograniczona powierzchnia płaska o jednym wierzchołku oraz o brzegu złożonym z dwóch półprostych o początku w tym właśnie wierzchołku.
- Część wspólna (w przypadku kąta wypukłego) lub suma (w przypadku kąta wklęsłego i pełnego) dwóch półpłaszczyzn wyznaczonych przez proste nierównoległe (wtedy punkt przecięcia tych prostych jest wierzchołkiem kąta) albo nakładające się.

- zerowy - jego ramiona nakładają się, ma miarę 0°, geometrycznie ma kształt półprostej,
- półpełny - jego ramiona przedłużają się tworząc prostą, ma miarę 180°, geometrycznie ma kształt półpłaszczyzny,
- prosty - połowa kąta półpełnego, ma miarę 90°,
- pełny - suma dwóch kątów półpełnych, których częścią wspólną są jedynie ramiona, ma miarę 360°, geometrycznie ma kształt płaszczyzny z wyróżnionym punktem (wierzchołkiem),
- ostry - każdy kąt mniejszy do kąta prostego; ma miarę od 0° do 90°,
- rozwarty - każdy kąt większy od kąta prostego i mniejszy od półpełnego, ma miarę od 90° do 180°,
- wypukły - każdy kąt, który jest figurą wypukłą, ma miarę od 0° do 180° albo jest kątem pełnym,
- wklęsły - każdy kąt, który jest figurą wklęsłą, ma miarę od 180° do 360°,
- nieskierowany - kąt, w którym nieistotny jest kierunek mierzenia rozwartości, nazywany jest po prostu kątem;
- skierowany - kąt, w którym istotny jest kierunek, w jakim mierzymy rozwartość (tzn. jedno ramię jest początkowe, a drugie końcowe); różnica między kątem nieskierowanym i skierowanym jest podobna do różnicy między odcinkiem i wektorem (wektor ma punkt początkowy i końcowy, a odcinek ma 2 końce, które niczym się nie różnią);
- dodatni (skierowany dodatnio) - kąt skierowany, w którym rozwartość mierzymy w kierunku przeciwnym do kierunku ruchu wskazówek zegara;
- ujemy (skierowany ujemnie) - kąt skierowany, w którym rozwartość mierzymy w kierunku zgodnym do kierunku ruchu wskazówek zegara;
- obrotu - kąt skierowany, mierzący obrót figury względem jakiegoś punktu płaszczyzny lub względem prostej w przestrzeni,
- rozwarcia (np. stożka) - kąt wyznaczony przez powierzchnię (boczną np. stożka) na płaszczyźnie przekroju osiowego.
Kąty mogą być:
- przyległe - każde dwa kąty o wspólnym ramieniu i wierzchołku oraz rozłącznych wnętrzach dopełniające się do kąta półpełnego, na rysunku poniżej np. kąty 1-2;
- wierzchołkowe - każde dwa wypukłe kąty o wspólnym wierzchołku, których ramiona przedłużają się wzajemnie tworząc proste, kąty wierzchołkowe mają równe miary, na rysunku poniżej np. kąty 1-3;
- naprzemianległe i odpowiadające - pary kątów utworzonych przez przecięcie dwóch różnych prostych trzecią prostą; na rysunku poniżej kąty 1-7 oraz 2-8 to kąty naprzemianległe zewnętrzne, a kąty 6-4 oraz 3-5 to kąty naprzemianległe wewnętrzne, pary 7-3, 6-2, 8-4 i 5-1 to kąty odpowiadające, pary 8-1 i 7-2 to kąty jednostronnie zewnętrzne, a pary 5-4 i 6-3 to kąty jednostronnie wewnętrzne.

- przy podstawie (np. trójkąta równoramiennego) - kąt między półprostymi wyznaczonymi przez podstawę wielokąta oraz bok wielokąta sąsiadujący z podstawą;
- wewnętrzne (wielokątów) - kąty, na których ramionach leżą sąsiednie boki wielokąta, wierzchołek wielokąta jest wierzchołkiem kąta, a wnętrze wielokąta zawiera się we wnętrzu kąta, np. kąty α, β, γ w trójkącie z poniższego rysunku;

- zewnętrzne (wielokątów) - kąty przyległe do kątów wewnętrznych wielokąta, np. kąty α, β, γ w trójkącie z poniższego rysunku;

Kąty związane z okręgiem:
- kąt środkowy - wierzchołek znajduję się w środku okręgu; mówimy, że kąt środkowy jest oparty na łuku AB, jeśli punkty A i B są przecięciami okręgu i ramion kąta, a łuk AB leży we wnętrzu kąta;

- kąt wpisany w okrąg - wierzchołek znajduje się na okręgu, a każde z jego ramion przecina okrąg; mówimy, że kąt wpisany jest oparty na łuku AB, jeśli punkty A i B są przecięciami okręgu i ramion kąta, a łuk AB leży we wnętrzu kąta (tzn. wierzchołek kąta wpisanego leży poza łukiem AB);
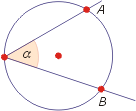
- kąt dopisany - kąt wypukły zawarty między półprostą zawierającą cięciwę okręgu a prostą styczną do okręgu w punkcie będącym jednym z końców tej cięciwy; mówimy, że kąt dopisany jest oparty na łuku AB, jeśli punkty A i B są końcami cięciwy, a łuk AB leży we wnętrzu kąta;
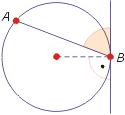
- kąt między stycznymi do okręgu - kąt między półprostymi wyznaczonymi przez punkt przecięcia stycznych do okręgu w punktach będących końcami cięciwy niebędącej średnicą oraz punkty styczności; mówimy, że kąt ten jest oparty na obu łukach AB, gdzie punkty A i B są przecięciami okręgu i ramion kąta;
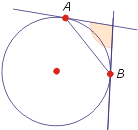
- kąt między siecznymi okręgu - kąt między prostymi przecinającymi się w punkcie leżącym poza okręgiem (wewnątrz lub na zewnątrz) i przecinającymi okrąg w dwóch punktach każda; mówimy, że kąt ten jest oparty na obu łukach AC i BD, gdzie punkty A i B oraz C i D są przecięciami okręgu z każdą z prostych;
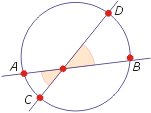

Kontrprzykłady:
- żaden ograniczony obszar płaszczyzny nie jest kątem;
- powierzchnia wycięta ze stożka przez dwie tworzące (nie jest powierzchnią płaską);
- sam brzeg bez wnętrza kąta

- samo wnętrze bez brzegu kąta

- Kąty wierzchołkowe są przystające.
- Kąty naprzemianległe są przystające wtedy i tylko wtedy, gdy dwie proste przecięte trzecią są równoległe.
- Kąty odpowiadające są przystające wtedy i tylko wtedy, gdy dwie proste przecięte trzecią są równoległe.
- Suma kątów jednostronnie wewnętrznych (lub jednostronnie zewnętrznych) jest kątem półpełnym wtedy i tylko wtedy, gdy dwie proste przecięte trzecią są równoległe.
- Suma miar kątów wewnętrznych w dowolnym trójkącie wynosi 180°, a w czworokącie 360°.
- Suma miar kątów wewnętrznych w dowolnym n-kącie wypukłym jest równa (n-2)·180º.
- Kąt zewnętrzny w trójkącie jest sumą kątów wewnętrznych do niego nieprzyległych.
- Suma miar kątów zewnętrznych w dowolnym wielokącie wypukłym jest równa 360º.
- Kąty przy podstawie trójkąta lub trapezu równoramiennego są przystające.
- Czworokąt można wpisać w okrąg wtedy i tylko wtedy, gdy suma miar przeciwległych kątów jest równa 180°.
- Miara kąta środkowego jest dwa razy większa niż miara kąta wpisanego opartego na tym samym łuku.
- Miary kątów wpisanych opartych na przystających łukach są równe.
- Miara kąta dopisanego jest równa mierze kąta wpisanego opartego na tym samym łuku.
- Miara kąta między stycznymi jest różnicą miar kątów wpisanych opartych na tych samych łukach, co ten kąt.
- Miara kąta między siecznymi jest sumą (gdy wierzchołek kąta leży wewnątrz okręgu) lub różnicą (gdy wierzchołek kąta leży na zewnątrz okręgu) miar kątów wpisanych opartych na tych samych łukach co ten kąt.
Konstruowalne cyrklem i linijką są jedynie kąty o miarach $\frac{360^\circ}{n}$, gdzie n = 2kp1...ps (k jest liczbą całkowitą nieujemną, zaś pi są różnymi liczbami pierwszymi Fermata - są nimi np. liczby 3, 5, 17). To znaczy, że jest konstruowalny np. kąt o mierze $\frac{360^\circ}{17}$≈21,18°, a nie jest np. kąt o mierze 21o.
Cyrklem i linijką nie da się skonstruować jednej trzeciej części dowolnego kąta (innymi słowy nie da się podzielić konstrukcyjnie dowolnego kąta na 3 przystające części, czyli skonstruować trójsiecznych tego kąta). Jest to możliwe tylko w przypadku szczególnych kątów, np. 180° lub 90°.
- Kąt między prostymi na płaszczyźnie to każdy z kątów utworzonych przez półproste zawarte w tych prostych.
- Kąt między odcinkami to każdy z dwóch kątów między prostymi zawierającymi te odcinki.
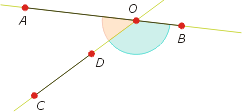
- Kąt między wektorami - każde dwa wektory można przesunąć równolegle (takie przesunięcie nie zmienia kąta nachylenia) tak, aby miały wspólny początek; każdy wektor wyznacza półprostą o początku w początku wektora przechodzącą przez koniec wektora - kąt między wektorami to wypukły kąt między tymi właśnie półprostymi.
- Kąt między prostymi w przestrzeni to kąt między dowolnymi wektorami równoległymi (lub prostopadłymi) do tych prostych (ten kąt można znaleźć nawet jeśli proste się nie przecinają).
- Kąt między płaszczyznami w przestrzeni to kąt między wektorami prostopadłymi do tych płaszczyzn (inaczej mówiąc jest to kąt płaski utworzony w przecięciu tych płaszczyzn płaszczyzną do nich obu prostopadłą). W matematyce szkolnej taki kąt nazywa się czasem dwuściennym, ale to nie jest poprawna nazwa, gdyż kąt dwuścienny nie jest płaski.
Mierzenie rozwartości kątów
Jednostki:
- stopień [°] - kąt o rozwartości 1° to jedna trzystasześćdziesiąta część kąta pełnego;
- radian [rad] - kąt o rozwartości 1 radiana (najczęściej mówi się tylko "o rozwartości jeden") to kąt, który z okręgu jednostkowego o środku w wierzchołku tego kąta wycina łuk długości 1;
- gradus, grad [cD lub g] - kąt o rozwartości 1g to setna część kąta prostego.
Związki między jednostkami:
- π (rad) = 180°,
- 1g = 0,9° = π/200 (rad)
Do pomiaru rozwartości kąta służy kątomierz (analogowy lub elektroniczny).
Każdy kąt można umieścić w układzie współrzędnych tak, aby jego wierzchołek znajdował się w początku układu współrzędnych, a jedno z ramion pokrywało się z dodatnia półosią osi OX. Jeżeli obszar kąta rozpościera się na lewo od obserwatora znajdującego się w początku układu i zwróconego twarzą w dodatnią stronę osi OX, to miara tego kąta jest dodatnia, a jeżeli obszar kąta rozpościera się na prawo od obserwatora, to umownie miarę tego kąta podajemy z minusem.
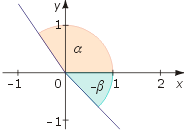
α = 120º, β = -60º
Badanie rozwartości kątów
Na każdym kącie większym od zerowego i mniejszym od półpełnego można zbudować trójkąt, łącząc dowolny punkt jednego ramienia z dowolnym punktem drugiego ramienia (bez wierzchołka).

- Kąt trójkąta jest ostry, jeśli nie leży naprzeciwko najdłuższego boku.
- Kąt α trójkąta jest prosty, jeśli długości boków spełniają b2 + c2 = a2. Pozostałe kąty trójkąta są ostre.
- Kąt α trójkąta jest rozwarty, jeśli długości boków spełniają b2 + c2 < a2. Pozostałe kąty trójkąta są ostre.
- Kąt α trójkąta jest ostry, jeśli długości boków spełniają b2 + c2 > a2.
Obliczanie rozwartości kątów:
- Rozwartość kątów w trójkącie prostokątnym możemy obliczyć znając długości boków tego trójkąta i wykorzystując funkcje trygonometryczne.
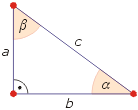
β = arcsin (b/c)
- Rozwartość kątów w dowolnym trójkącie możemy obliczyć z twierdzenia kosinusów:
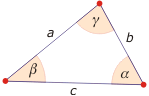 α = arccos$\frac{b^2+c^2-a^2}{2bc}$
α = arccos$\frac{b^2+c^2-a^2}{2bc}$
β = arccos$\frac{a^2+c^2-b^2}{2ac}$
γ = arccos$\frac{a^2+b^2-c^2}{2ab}$
- Rozwartość kątów w dowolnym trójkącie możemy obliczyć z twierdzenia sinusów:
R - promień okręgu opisanego na trójkącie
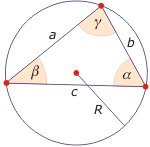 α = arcsin$\frac{a}{2R}$
α = arcsin$\frac{a}{2R}$
β = arcsin$\frac{b}{2R}$
γ = arcsin$\frac{c}{2R}$
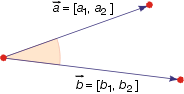
- Rozwartość kąta między wektorami o podanych współrzędnych możemy obliczyć, korzystając z iloczynu skalarnego tych wektorów:

$$ \cos \angle ( \vec{a}, \vec{b})= \frac{\vec{a} \circ \vec{b}}{\mid \vec{a} \mid \cdot \mid \vec{b} \mid} = \frac{a_1 b_1 + a_2 b_2}{\sqrt{a^2_1 + a^2_2} \cdot \sqrt{b^2_1 + b^2_2}} $$
- Rozwartość kąta między wektorami o podanych współrzędnych możemy obliczyć, korzystając z wyznacznika wektorów:
$$\sin \angle (\vec{a}, \vec{b}) = \frac{ \det( \vec{a}, \vec{b})}{\mid \vec{a} \mid \cdot \mid \vec{b} \mid} = \frac{a_1 b_2 - a_2 b_1}{\sqrt{a^2_1 + a^2_2} \cdot \sqrt{b^2_1 + b^2_2}} $$
- Euklides w V w. p.n.e. za kąty uważał tylko kąty wypukłe (czyli o rozwartościach od 0o do 180o).
- Al-Kaszi w XV wieku tak definiował kąt płaski: to, co ograniczone jest przez dwie linie proste, przecinające się w jednym punkcie i nie zlewające się w jedną.
- dwusieczna kąta
- kąt bryłowy
- kąt dwuścienny
- steradian
Bibliografia:
- Encyklopedia szkolna. Matematyka, WSiP, Warszawa 1989.
- Leksykon matematyczny, Wiedza Powszechna, Warszawa 1993.
- Witold Więsław, Matematyka i jej historia, Nowik, Opole 1997.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
