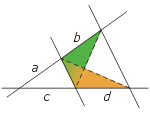
Właściwie cała szkolna (i nie tylko) geometria opiera się na własnościach trójkątów podobnych i twierdzeniu Talesa. Choć są to elementarne fakty znane każdemu gimnazjaliście, korzysta się z nich także w najbardziej zaawansowanych problemach syntetycznej geometrii i w wielu zadaniach olimpijskich.
Do boju z Talesem
2 komentarze
Czytaj dalej
2007 i podzielność
Znane są dość skomplikowane wzory na sumy potęg kolejnych liczb naturalnych, np.
[TEX] 1^7+2^7+3^7+\ldots+n^7=\frac{1}{8}n^8+\frac{1}{2}n^7+\frac{7}{12}n^6-\frac{7}{24}n^4+\frac{1}{12}n^2[/TEX]Jednak takie wzory nie będą potrzebne do rozwiązania przestawionych zadań dotyczących podzielności; można znaleźć radykalnie prostsze rozumowania.
Proste i okręgi
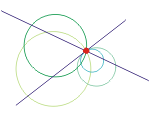Proste i okręgi to jedne z najprostszych figur geometrycznych, a jednocześnie to jedyne figury płaskie już od czasów starożytnych uznawane za doskonałe (tylko one mogą ślizgać się same po sobie). Do dziś obowiązuje kanon konstrukcji geometrycznych wykonywanych cyrklem i linijką, zatem sprowadzających się do kreślenia wyłącznie prostych i okręgów. Zbadajmy wzajemne relacje, jakie zachodzą między tymi figurami.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
