To chyba najprostsza z brył wykonanych w technice origami, jaką można sobie wyobrazić, dlatego polecamy ją wszystkim początkującym, leniwym, zabieganym, posiadającym "dwie lewe ręce" lub dowolną kombinację tych cech. Na dodatek dla otrzymanego foremnego ośmiościanu można znaleźć rozmaite zastosowania, nie tylko na lekcjach matematyki.
Pomysłodawcą wykorzystania prostej kwadratowej bazy do zbudowania modelu ośmiościanu foremnego jest znany origamista Robert Neale.
Jest to model wierzchołkowy, dlatego wykonujemy go z 6 jednakowych modułów (ośmiościan foremny ma wszak 6 wierzchołków). Potrzebnych jest w tym celu 6 jednakowych kwadratowych kartek dowolnej wielkości i wolne 5-10 minut. Początkującym origamistom będzie znacznie łatwiej, jeśli każda kartka będzie w innym kolorze. W końcowej fazie pracy może im się przydać się także druga para rąk do pomocy w przytrzymaniu konstrukcji.
Każdą kartkę osobno zaginamy wzdłuż wszystkich osi symetrii kwadratu (rys. 1 i 2) formując rozgwiazdę (rys. 3). I to właściwie już koniec.
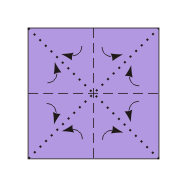
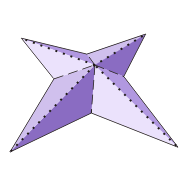
Powstałych 6 elementów nasuwamy jeden na drugi, po dwa z każdego z trzech prostopadłych kierunków (jeden z góry, drugi z dołu, trzeci z przodu, czwarty z tyłu, piąty z prawej, szósty z lewej) uważając, aby co drugie ramię rozgwiazdy wypadało na wierzchu, a co drugie wewnątrz konstrukcji (rys. 4 i 5). Ostateczny efekt widzimy na zdjęciu poniżej.
Okazuje się, że nawet taka prosta forma może znaleźć rozmaite zastosowania, np. jako:
- poglądowy model ośmiościanu foremnego z poprowadzonymi płaszczyznami symetrii,
- ilustracja modelu przestrzennego kartezjańskiego układu współrzędnych prostokątnych (z oktantami, jako odpowiednikami ćwiartek układu na płaszczyźnie),
- bączek probabilistyczny lub (jak kto woli) ośmiościenna kostka do gry.
Zatrzymajmy się nad tym ostatnim pomysłem. Oczywiście wszystkie wielościany foremne nadają się na kostki do gry, gdyż prawdopodobieństwo ich upadku na każdą ze ścian jest takie samo, jednak nie wszystkie są równie wygodne. Na przykład jeśli rzucamy czworościanem foremnym i upadnie on na jedną ze ścian, to nie bardzo wiadomo, z której ściany odczytać wynik.
Inaczej jest z kostką sześcienną, która ma ściany parami równoległe i jeśli upadnie na jedną ścianę, to zawsze istnieje „wierzchnia” ściana równoległa do podłoża, z której odczytujemy wynik. Tę wygodną dla gier losowych własność sześcian zawdzięcza temu, że jest graniastosłupem – jedynym wśród brył foremnych. Natomiast ośmiościan foremny jest jedynym foremnym antygraniastosłupem (zwanym też graniastosłupem skręconym), co również czyni zeń wygodną kostkę do gry, gdyż każda ściana ma swoją przeciwległą ścianę równoległą (dokładne przeanalizowanie tego problemu pozostawiamy Czytelnikom). Na naszym modelu wystarczy więc odpowiednio ponumerować wszystkie zagłębienia i kręcąc nim jak bączkiem lub podrzucając jak kostką do gry, otrzymywać losowe wyniki ze zbioru {1, 2, 3, …, 8}.
Polecane strony:
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Geometria zwana świętą
Tu jest dużo o wielościanach foremnych:
http://www.cheops.darmowefora.pl/index.php?topic=272.0.
Pozdrawiam
To jest świetne!
Zrobiłam już dwa takie osmiościany. Są przecudne i proste :) bardzo łatwe do zrobienia. Gorąco polecam.
Fajoska zabawa
Fajoska zabawa. Wciąga. Nauczę swoje dzieciaki na obozie matematycznym, który organizuję z koleżanką w tym roku. Może zrobimy jakieś zawody...
Zagadka
Jak z modułów sonobe wykonać taki sam model ośmiościanu foremnego?
Wskazówka
Ośmiościan gwiaździsty dla leniwych
A jak je połączyć?
Jak połączyć te 6 modułów wywiniętych "na lewą stronę"? Proszę o odpowiedź, bo chciałbym coś takiego złożyć, a jestem początkującym origamistą. Z góry DZIĘKI :-)
Instrukcja składania
Najpierw należy "wywrócić na lewą stronę" każdy moduł z osobna. Jak to zrobić? Przygotowaną wg pierwotnej instrukcji rozgwiazdę trzeba położyć na stole głównym wierzchołkiem do góry i delikatnie naciskać na ów wierzchołek, aż z górki zrobi się dołek; następnie odwrócić moduł na drugą stronę, by znowu leżał "górką" do góry. To jest nasz nowy moduł, a strona, którą teraz widać z góry, będzie skierowana na zewnątrz bryły. Moduł ten jest podzielony na cztery "kwadratowe" skrzydełka (jedno żółte można zobaczyć na froncie bryły ze zdjęcia wyżej). Skrzydełka modułów nakładamy jedne na drugie tak, by co drugie skrzydełko z danego modułu wypadło na zewnątrz, a co drugie wewnątrz bryły. Model jest delikatny i uzyskuje stabilność dopiero po dołożeniu ostatniego elementu. Powodzenia!