Zadania
Zad. 1. (typ humanistyczny) Obliczyć krawędź podstawową ostrosłupa prostego, którego podstawa jest trójkątem równobocznym, wysokość tego ostrosłupa wynosi w = √3 m, zaś krawędź boczna jest o 1 mniejszą od krawędzi podstawowej.
Zad. 2. (typ klasyczny) Objętość prostopadłościanu V = 990 cm3, powierzchnia tej bryły równa się P = 598 cm2, obwód podstawy O = 38 cm. Znaleźć krawędzie prostopadłościanu.
Zad. 3. (typ klasyczny i humanistyczny) Rozwiązać równania:
x3 + y3 = [tex]\frac{35}{36}[/tex]x2y2
x + y = 5.
Szkice rozwiązań
Zad. 1.
Przyjmując oznaczenia jak na rysunku, wiemy, że
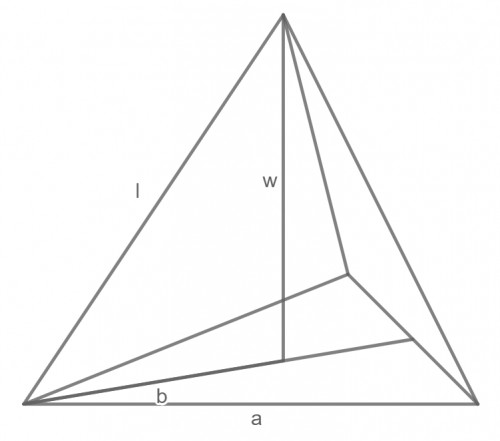
w = [tex]\sqrt{3}[/tex] oraz l = a - 1.
Wykreślając trójkąt zawierający krawędź boczną, wysokość i część wysokości podstawy ostrosłupa, otrzymamy
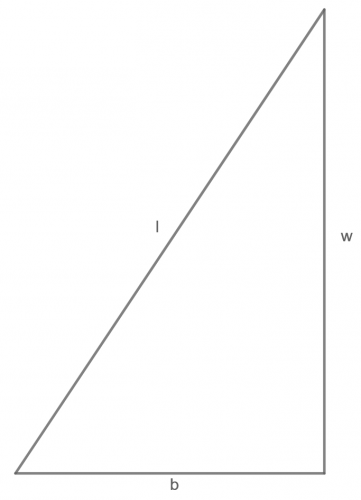
Z twierdzenia Pitagorasa dla powyższego trójkata mamy:
w2 + b2 = l2.
Skoro b = a[tex]\frac{\sqrt{3}}{3}[/tex] (dlaczego?), w = [tex]\sqrt{3}[/tex] oraz l = a - 1, to równanie to można uprościć do postaci
a2 - 3a - 3 = 0, które to równanie ma tylko jedno możliwe rozwiązanie spełaniające warunki zadania (jakie warunki?).
Zatem długość krawędzi podstawy wynosi [tex]\frac{3+\sqrt{21}}{2}[/tex].
Zad. 2.
Przyjmując oznaczenia jak na rysunku, otrzymujemy układ równań:
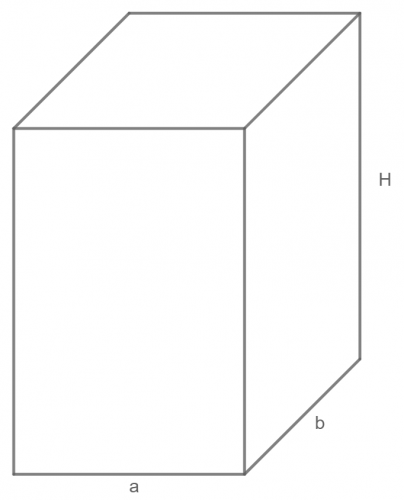
abH = 990
2(ab + aH + bH) = 598
2a + 2b = 38.
Po podstawieniu do drugiego równania H wyliczonego z pierwszego oraz a wyliczonego z trzeciego dostajemy po oproszczeniu równanie:
a2b2 - 299ab + 18810 = 0.
Jest ono spełnione przez ab = 90 oraz ab = 209.
Przypadek pierwszy prowadzi do a = 9, b = 10, H = 11. natomiast drugi - do sprzeczności.
Stąd krawedzie tego prostapadłościanu mają długości 9, 10 i 11.
Zad. 3.
Zauważmy, że korzystając ze wzoru skrócenego mnożenia dla trzeciej potęgi sumy otrzymujemy po uporządkowaniu:
125 = (x + y)3 = x3 + y3 + 3xy(x+y) = [tex]\frac{35}{36}[/tex]x2y2 + 15xy.
Podstawiając a = xy, otrzymujemy równanie kwadratowe, które daje dwa rozwiązania:
a = 6 i a = [tex]-\frac{150}{7}[/tex].
W pierwszym przypadku otrzymujemy x= 2, y = 3 lub odwrotnie,
w drugim zaś x = [tex]\frac{5+\sqrt{\frac{31}{7}}}{2}[/tex], y = [tex]\frac{5-\sqrt{\frac{31}{7}}}{2}[/tex] lub odwrotnie.

 Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć? Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
 Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera.
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 

