Zadania
Zad. 1. (typ klasyczny) Wyznaczyć postęp geometryczny, jeśli:
a1 + a2 + a3 = 21
a2 – a3 = 3.
Zad. 2. (typ humanistyczny) Rozwiązać równanie: 1/(5–log x) + 2/(1+log x) = 1.
Zad. 3. (typ klasyczny) Oblicz promienie obu podstaw (R = x, r = y) stożka prostego ściętego, jeżeli dane:
objętość V = 378 [tex]\pi[/tex] m3
wysokość w = 6 m
różnica promieni R–r = 9 m.
Szkice rozwiązań
Zad. 1.
Raz dodając, a raz odejmując powyższe równania, otrzymujemy układ:
a1 + 2a2 = 24
a1 + 2a3 = 18.
Korzystając ze wzoru ogólnego na n-ty wyraz ciągu geometrycznego i wyliczając z pierwszego równania iloraz ciągu, otrzymujemy po przekształceniu:
a12 - 28a1 + 192 = 0.
Równanie to spełniają liczby 12 i 16, a dla każdej z nich możemy wyznaczyc brakujące dwa elementy ciągu.
Zatem odpowiedzią są ciągi (12, 6, 3) oraz (16, 4, 1).
Zad. 2.
Załóżmy, że mianowniki obu ułamków sa rózne od zera. Wówczas po wymnożeniu rówanania przez oba mianowniki otrzymujemy:
(1+log x) + 2(5–log x) = (5–log x)(1+log x), co możemy przekształcić do postaci:
log2x - 5log x + 6 = 0, co daje log x = 2 lub log x = 3. Oba te rozwiązania należą do dziedziny.
Zatem pierwotne równanie spełnia e2 i e3.
Zad. 3.
Uzupełniając opisany w zadaniu ścięty stożek do pełnego stożka i uznaczając, jak na rysunku wysokośc odciętej częsci stożka u, otrzymujemy:
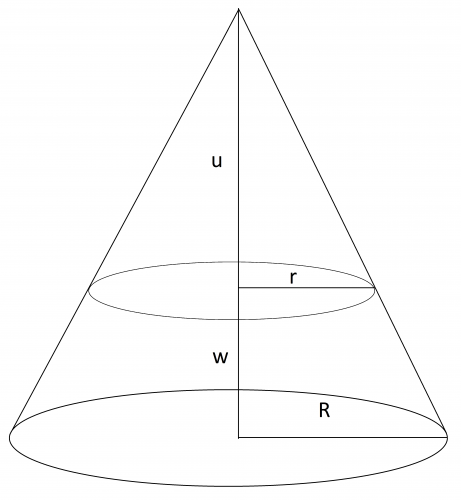
378 [tex]\pi[/tex] m3 = [tex]\frac{1}{3}[/tex]((u+w)[tex]\pi[/tex]R2 - u[tex]\pi[/tex]r2).
Z podobieństwa trójkątów wyznaczonych przez wysokości stożka i promienie podstaw wiemy, że
[tex]\frac{u}{w} = \frac{r}{R-r}[/tex], co po podstawieniu danych z treści zadani pozwala stwierdzić, że
[tex]\frac{u}{r} = \frac{u+w}{R} = \frac{2}{3}[/tex].
Zauważmy, że, upraszczając i dodając do równania wyrażającego objętość wyrażenia -(u+w)r2 + (u+w)r2, otrzymamy równanie niższego rzędu:
1134 = (u+w)R2 - (u+w)r2 + (u+w)r2 - ur2 =
= (u+w)(R2 - r2) + wr2 =
= (u+w)(R-r)(R+r) + 6r2 =
= 9(u+w)(R+r) + 6r2.
Ponadto, skoro 3(u+w) = 2R oraz R = 9+r, to
378 = 2(9+r)(9+2r) + 2r2, czyli
r2 + 9r - 36 = 0.
Stad r = 3 (dlaczego jest jedno rozwiązanie?) oraz R = 12.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
