Żeby rozwiązać nierówność kwadratową jednej z postaci
- ax2+bx+c < 0,
- ax2+bx+c ≤ 0,
- ax2+bx+c > 0,
- ax2+bx+c ≥ 0,
- ax2+bx+c ≠ 0,
trzeba najpierw rozwiązać równanie ax2+bx+c = 0, co opisano tutaj.
Następnie szkicujemy wykres paraboli, której wzór analityczny stanowi lewą stronę równania i rozwiązanie nierówności odczytujemy z tego wykresu. Przy szkicowaniu wykresu paraboli należy wziąć pod uwagę jej następujące własności:
- wykres przecina oś OX w miejscach, które są pierwiastkami równania,
- ramiona paraboli są skierowane w górę dla a>0 lub w dół dla a<o,
- parabola ma wierzchołek na linii pionowej przecinającej oś OX pośrodku między miejscami zerowymi,
- parabola jest symetryczna względem pionowej prostej przechodzącej przez jej wierzchołek.
Przykłady
- x2+4x+3 < 0
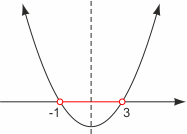
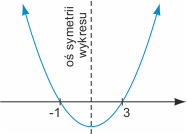Rozwiązujemy równanie x2+4x+3 = 0. Otrzymujemy dwa pierwiastki: -1 oraz 3. Ponieważ współczynnik a przy x2 jest dodatni (wynosi 1), ramiona paraboli są skierowane do góry, a wykres prawej strony nierówności wygląda tak, jak na rysunku obok. Widać z niego, że wartości mniejsze od zera są przyjmowane pomiędzy pierwiastkami czyli na przedziale (-1, 3) i ten przedział jest szukanym rozwiązaniem nierówności. - x2 + 3x - 5 > 0
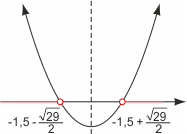Rozwiązujemy równanie x2+3x-5 = 0. Otrzymujemy dwa pierwiastki: -1.5 - √29/2 ≈ -4,2 oraz -1.5 + √29/2 ≈ 1,2. Ponieważ współczynnik a przy x2 jest dodatni (wynosi 1), ramiona paraboli są skierowane do góry, a wykres prawej strony nierówności wygląda tak, jak na rysunku obok. Widać z niego, że wartości większe od zera są przyjmowane pomiędzy ujemną nieskończonością a pierwszym pierwiastkiem oraz pomiędzy drugim pierwiastkiem a dodatnią nieskończonością, czyli na zbiorze (-∞, -1.5-√29/2)[tex]\cup[/tex](-1.5+√29/2, ∞) i ten zbiór jest szukanym rozwiązaniem nierówności. - -3x2 + 4x + 2 < 0
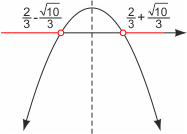Rozwiązujemy równanie -3x2+4x+2 = 0. Otrzymujemy dwa pierwiastki: 2/3 - √10/3 ≈ -0,4 oraz 2/3 + √10/3 ≈ 1,7. Ponieważ współczynnik a przy x2 jest ujemny (wynosi -3), ramiona paraboli są skierowane w dół, a wykres prawej strony nierówności wygląda tak, jak na rysunku obok. Widać z niego, że wartości mniejsze od zera są przyjmowane pomiędzy ujemną nieskończonością a pierwszym pierwiastkiem oraz pomiędzy drugim pierwiastkiem a dodatnią nieskończonością, czyli na zbiorze (-∞, 2/3-√10/3)[tex]\cup[/tex](2/3+√10/3, ∞) i ten zbiór jest szukanym rozwiązaniem nierówności.
Zadania do samodzielnego rozwiązania
1) x2 ≥ 4
2) x2 < 2
3) x2-5x ≥ 0
4) -2x2+5x >0
5) x2+3x-5 > 0
6) -2x2+4x+2 < 0
7) -3x2+4x+2 ≤ 0
8) (x-3)(x+2) > (x-1)2+2
9) (x-3)(x+3) ≤ (x+4)2-3x
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
