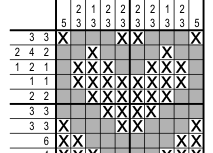
W artykule Tuzin dwunastościanów wspominaliśmy, że dwunastościan rombowy (rys. 1) ma wiele ciekawych własności.
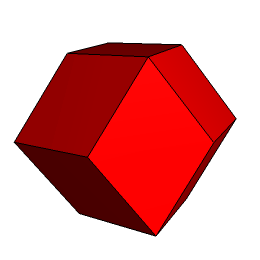
W tym miejscu prezentujemy interesującą łamigłówkę związaną z tą bryłą. Składa się ona z sześciu przystających klocków (rys. 2, 3).
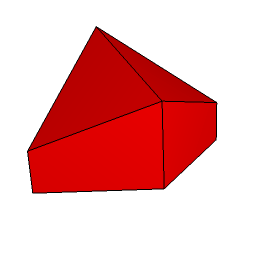
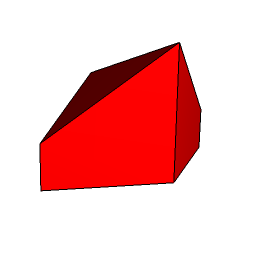
Rys. 2 (widok "z przodu") Rys. 3 (widok "z tyłu")
Z łatwością można je wykonać samodzielnie. Kliknięcie w poniższy link otwiera w nowym oknie siatkę takiego elementu.
Z sześciu klocków można ułożyć zarówno dwunastościan rombowy jak i graniastosłup prawidłowy sześciokątny (rys. 4).
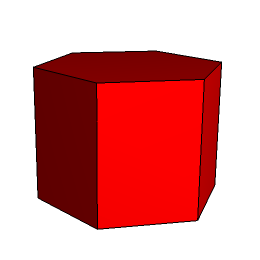
Rys. 4
Po uporaniu się z tymi problemami można zmierzyć się z dodatkowym zadaniem - wyznaczyć stosunek długości krawędzi bocznej do krawędzi podstawy w tym graniastosłupie.
Łamigłówka ta w oczywisty sposób pokazuje, że dwunastościan rombowy można pociąć na skończenie wiele wielościennych części, z których da się złożyć pewien graniastosłup prawidłowy sześciokątny. Można sformułować problem ogólny: czy mając dwa wielościany o równych objętościach jest możliwe pocięcie jednego z nich na skończoną ilość wielościanów, z których da się zbudować tę drugą bryłę.
W 1900 roku David Hilbert umieścił ten problem na liście 23 najistotniejszych zadań stojących przed matematyką u progu XX wieku. Część zagadnień z jego listy do tej pory czeka na rozwiązanie, ale akurat ten problem został rozstrzygnięty bardzo szybko. Jeszcze w tym samym roku uczeń Hilberta - Max Dehn - podając kontrprzykład, wykazał, że nie zawsze jest to możliwe. Wiadomo na przykład, że czworościanu nie da się pociąć tak, by z otrzymanych wielościanów można było złożyć sześcian.
Inaczej rzecz ma się na płaszczyźnie. Na początku XIX wieku wykazano, że mając dane dwa wielokąty o równych polach można pociąć jeden z nich na mniejsze wielokąty i zbudować z nich ten drugi (twierdzenie to nosi nazwę twierdzenia Bolayi-Gerwiena). Więcej na ten temat piszemy na Portalu tutaj.
Wizerunki wielościanów zostały wyeksportowane z programu Great Stella. Siatka została przygotowana przy użyciu programu Wingeom.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
