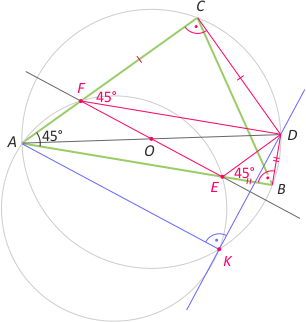
Zad. 1. W trójkącie ABC kąt A ma 45°. Niech AD będzie średnicą okręgu opisanego na trójkącie. Na bokach AB i AC obrano odpowiednio punkty E i F tak, że |DB|=|BE| oraz |DC|=|CF|. Niech K oznacza drugi punkt wspólny okręgów opisanych na trójkątach ABC i AEF. Wykaż, że prosta EF dzieli odcinek DK na połowy.
Zad. 2. Dany jest równoległobok ABCD. Okrąg dopisany do trójkąta ABD jest styczny do prostych AB i AD w punktach odpowiednio M i N. Wykaż, że punkty przecięcia odcinka MN z bokami BC i CD leżą na okręgu wpisanym w trójkąt BCD.
Zad. 3. W trójkącie ABC kąt B ma 30°, a kąt AMC ma 45° (M jest środkiem BC). Oblicz miarę kąta CAM.
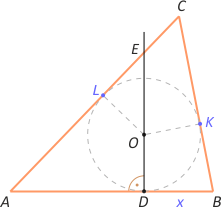
Zad. 4. (wolna amerykanka) W trójkąt ABC wpisano okrąg o środku O styczny do boku AB w punkcie D. Prosta DO przecina bok AC w punkcie E. Długości boków wynoszą |AC|=6 i |AB|=5. Wiadomo też, że pole trójkąta ADE jest połową pola trójkąta ABC. Oblicz pole trójkąta ABC.
W tym miesiącu za zadania 1-3 punkty po 30 pkt. otrzymali: Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) oraz Marzena Wąsiewicz (nauczycielka z Kajetan).
Za zadanie 4 po 10 pkt. otrzymali: Dominik Bysiewicz, Robert Ciężabka, Radosław Górzyński, Elżbieta Grzechnik, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek oraz Marzena Wąsiewicz. Gratulacje!
Zad. 1. Zauważmy, że trójkąty EBD i FCD są prostokątne i równoramienne. Stąd zaś wynika, że
|∡DEB| = |∡CFD| = 45°, co oznacza, że czworokąt AEDF jest równoległobokiem i jego przekątna EF przechodzi przez środek okręgu O. Ponieważ O jest środkiem cięciwy EF i jednocześnie leży na symetralnej cięciwy AK, EF i AK są równoległe i EF jest linią średnią w trójkącie AKD, skąd wynika teza.
Zad. 2. Oznaczmy przez K punkt styczności okręgu dopisanego z bokiem DB. Zauważmy, że trójkat AMN jest równoramienny (|AM|=|AN|), a tym samym równoramienny jest trójkąt DQN. Mamy zatem |DN| = |DK| = |DQ|. Analogicznie |BK|=|BP|. Z kolei z podobieństwa trójkątów DQN i PCQ mamy |CQ|=|CP|. Oznacza to, że punkty K, P i Q są punktami styczności okręgu wpisanego w trójkąt DBC.

Zad. 3. Łatwo zauważyć, że |<MAB|=15°. Niech CH będzie wysokością w trójkącie ABC. Wówczas trójkat CHB jest ekierkowy, w którym |CH|=|CM|=|MB| i |<HCB|=60°. Mamy zatem trójkąt równoboczny CHM i równoramienny AHM, gdzie |MH|=|AH|. Zatem trójkąt prostokątny AHC jest równoramienny, skąd x = 30°.

Zad. 4. Zauważmy, że |AD| = 5–x, |AL| = 5–x, |CL| = 6–(5–x) = x+1, |CK| = x+1, |BK| = x, skąd |BC| = 2x+1. Z twierdzenia kosinusów w trójkącie ABC mamy cosA = (61–(2x+1)2)/60. Z drugiej strony cosA= |AD|:|AE|. Z założenia mamy (|AD|·|AE|·sinA)/2 = 15·sinA)/2, skąd |AD|·|AE| = 15 i dalej |AE| = 15/(5–x) oraz cosA = |AD|:|AE| = ((5–x)2)/15. Przyrównując wzory na cosA, otrzymujemy równanie (61–(2x+1)2)/60 = ((5–x)2)/15, skąd x = 2 (przy wyniku x = 5/2 trójkąt ABC byłby równoramienny, a nie jest). Ostatecznie ze wzoru Herona otrzymujemy SABC = 12.