Uwaga! Rozpoczynając od stycznia 2014, zadania Ligi Zadaniowej dla gimnazjów należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Rolnik Franciszek w poniedziałek rano zabronował połowę pola, a pod wieczór zabronował jeszcze 4 ha tego pola. We wtorek zabronował 1/3 pozostałej części pola. W środę Franciszek skończył bronować ostatni 8-hektarowy fragment pola. Jaka była powierzchnia tego pola?
Zad. 2. Udowodnij, że dla x>0 i y>0 prawdziwa jest nierówność [tex]\sqrt{xy}\geq \frac{2}{\frac{1}{x}+\frac{1}{y}}[/tex].
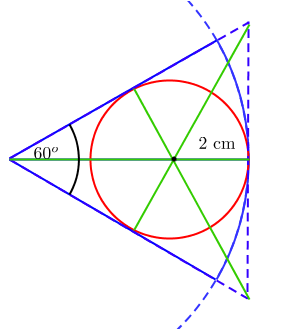
Zad. 3. W wycinek koła o promieniu 6 cm wyznaczony przez kąt środkowy o mierze 60o wpisano koło. Oblicz pole tego koła.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Bartosz Czyżewski GM 1 Jelenia Góra, Joanna Lisiowska KZE Warszawa, Ola Madrzańska GM ?, Klaudia Marcinkiewicz GM 24 Katowice, Maciej Pająk GM 13 Wrocław, Michał Stempniak GMSS Ostrów Wielkopolski i Wojciech Wiśniewski GM 3 Giżycko,
- 2 pkt. - Piotr Czekała GM 46 Szczecin i Mateusz Rzepecki GM 14 Wrocław,
- 1 pkt. - Monika Tomaszewska GM 3 Brzeg.
Pozostali uczestnicy zdobyli poniżej 1 punktu. Liga dopiero dobiega do półmetka, więc w ostatecznej klasyfikacji wszystko jest jeszcze możliwe.
Po czterech miesiącach Ligi z wynikiem 12 pkt. (na 12 możliwych) prowadzi Bartosz Czyżewski z GM 1 Jelenia Góra. Gratulujemy!
Zad. 1. Niech x oznacza szukaną powierzchnię pola w hektarach. Franciszek zabronował:
- w poniedziałek 0,5x+4,
- we wtorek (x-0,5x-4)/3,
- w środę 8.
Rozwiązując równanie x = (0,5x+4) + (0,5x-4)/3 + 8, otrzymamy x=32 ha.
Zad. 2. Przekształcamy daną nierówność w następujący sposób:
- mnożymy licznik i mianownik prawej strony przez xy (z założenia ≠0)
[tex]\sqrt{xy}\geq \frac{2xy}{x+y}[/tex] - mnożymy obie strony nierówności przez [tex]\frac{x+y}{\sqrt{xy}}[/tex] (wyrażenie to jest stale dodatnie)
[tex]x+y\geq \frac{2xy}{\sqrt{xy}}[/tex] - mnożymy licznik i mianownik prawej strony przez √(xy)/xy (z założenia ≠0)
[tex]x+y\geq 2\sqrt{xy}[/tex] - podnosimy obie strony do kwadratu (można to zrobić, bo obie są dodatnie)
(x+y)2 ≥ 4xy - przekształcamy tożsamościowo
x2+2xy+y2 ≥ 4xy, czyli x2-2xy+y2 ≥ 0, co jest równoważne (x-y)2 ≥ 0.
Ostatnia nierówność jest spełniona dla dowolnych liczb rzeczywistych, a wszystkie przejścia są równoważne, czyli można odwrócić kolejność przekształceń, co dowodzi prawdziwości wyjściowej nierówności. Udowodniliśmy w ten sposób nierówność pomiędzy średnią geometryczną (lewa strona) i harmoniczną (prawa strona) liczb dodatnich.
Zad. 3. Koło wpisane w wycinek większego koła jest identyczne z kołem wpisanym w trójkąt równoboczny o wysokości równej promieniowi wycinka, czyli 6. Wysokość ta jest jednocześnie środkową trójkąta i dwusieczną jego kąta, dlatego środek koła wpisanego w trójkąt (leżący w przecięciu dwusiecznych) dzieli tę wysokość w stosunku 2:1 (bo tak dzielą się środkowe w każdym trójkącie). Promień koła wpisanego stanowi więc 1/3 promienia wycinka i wynosi 2 cm. Zatem pole koła wpisanego w wycinek wynosi 4π.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
