Uwaga! Rozpoczynając od stycznia 2014, zadania Ligi Zadaniowej dla szkół podstawowych należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Dzieląc liczby 641 i 121 przez pewną liczbę, otrzymamy reszty z dzielenia równe odpowiednio 33 i 7. Znajdź liczbę, przez którą dzielono. Odpowiedź uzasadnij.
Zad. 2. Na pytanie: Która jest godzina? zagadnięty przechodzień odpowiedział: Pozostało jeszcze z doby ćwierć tego, co już upłynęło. Która to była godzina?
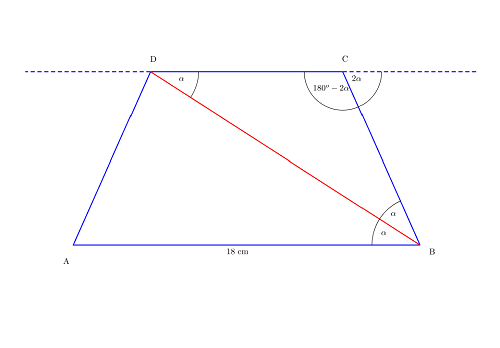
Zad. 3. W trapezie równoramiennym dłuższa podstawa ma 18 cm. Obwód trapezu jest równy 48 cm, a jego przekątna dzieli kąt ostry na połowy. Ile wynoszą długości pozostałych boków trapezu? Odpowiedź uzasadnij.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Zuzanna Banaś SP Bielany Wrocławskie, Antoni Bryszewski SP 15 Jelenia Góra, Gracjan Ciupa SSP 72 Wrocław, Hubert Cymbalista SP 1 Sobótka, Jakub Dobrzański SP 3 Lubin, Dominik Gąsior SP 52 Warszawa, Marek Hajduk SP 9 Lubin, Natalia Hydzik SP 5 Słupsk, Zuzanna Jóźków SP 1 Sobótka, Patrycja Karaś SP 15 Jelenia Góra, Marek Komorowski ZSP 5 Żory, Patrycja Krawczyk SP ?, Mateusz Lipiński SP 28 Wałbrzych, Nicoletta Litwin SP 15 Jelenia Góra, Stanisław Nowakowski SP 63 Wrocław, Zofia Ogonek SP 52 Warszawa, Magdalena Owczarek SSP Legionowo, Gabriela Poświata SSP Legionowo, Jakub Ptak SP 64 Wrocław, Aniela Reus SP 23 Wrocław, Filip Stachowiak SP 28 Wałbrzych, Oliwia Szczepańska SP Rogozino, Bartosz Szczerba SP 35 Szczecin, Adrianna Tomasik SP 2 Głuszyca i Michalina Więckowska SP 1 Konstancin-Jeziorna,
- 2,5 pkt. - Mikołaj Cholewiński SSP 35 Legionowo, Wojciech Pawłowski SP 63 Wrocław, Michał Piórkowski SP 63 Wrocław, Kinga Skorska SP ?, Amelia Szewc SP 1 Wołów i Michał Tłuczek SP 10 Głogów,
- 2 pkt. - Michał Jerzak SP 103 Warszawa, Oliwia Klebba SP Starzyno, Iwo Pilecki-Silva SP 76 Wrocław, Mikołaj Roszczyk SP 7 Legionowo, Marcin Siemieński SP 52 Warszawa, Wiktor Szywała SP 1 Sobótka i Mateusz Milewski SP 1 Bogatynia,
- 1,5 pkt. - Amadeusz Trzaska SP Świdnica,
- 1 pkt. - Mieszko Baszczak SP 301 Warszawa, Aleksandra Czarna SP 15 Jelenia Góra, Kamila Kwiatek SP Bielany Wrocławskie i Jan Staworzyński SP 15 Jelenia Góra.
Pozostałym uczestnikom Ligi przyznano poniżej 1 punktu. Liga dopiero dobiega do półmetka, więc w ostatecznej klasyfikacji wszystko jest jeszcze możliwe.
Po czterech miesiącach Ligi z wynikiem 11,5 pkt. (na 12 możliwych) prowadzi Zuzanna Banaś z SP w Bielanach Wrocławskich. Gratulujemy!
Zad. 1. Jeśli od liczb 641 i 121 odejmiemy odpowiednio reszty 33 i 7, to otrzymamy 608 i 114. Można je zapisać jako 608=2·2·2·2·2·19 oraz 114=2·3·19. Widać, że jedynym wspólnym dzielnikiem obu tych liczb większym od 33 (bo dzielnik musi być większy od reszty z dzielenia) jest 2·19=38. Jest to zatem liczba, przez którą dzielono 641 i 121.
Zad. 2. Według przechodnia aktualna godzina dzieliła dobę w stosunku 4:1. To znaczy, że upłynęło do tej pory 4/5 doby, co daje 4/5·24 = 96/5 = 191/5 = 1912/60. To znaczy, że była 19:12.
Zad. 3. Rozwiązanie przedstawia poniższy rysunek. Przekątna dzieli kąt ABC na połowy (o mierze α). Kąt BCD ma miarę 180°-2α (bo jest przyległy do kąta o mierze 2α). Z twierdzenia o sumie kątów w trójkącie kąt BDC też ma miarę α. To oznacza, że BCD jest trójkątem równoramiennym, czyli że krótsza podstawa trapezu ma taką samą długość jak jego ramiona, tzn |CD|=|BC|=|AD|. Obwód trapezu wynosi 18+3|CD|=48, skąd pozostałe boki trapezu mają po 10 cm.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
