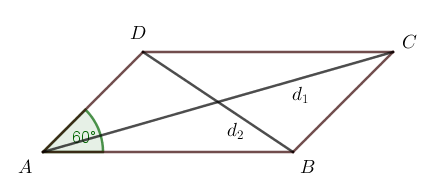
Zad.1. Dany jest równoległobok o kącie ostrym 60°. Wyznacz stosunek długości boków tego równoległoboku, jeśli stosunek kwadratów długości przekątnych wynosi 19/7.
Zad. 2. Znajdź wszystkie pary takich liczb, których iloczyn, suma oraz różnica kwadratów są równe.
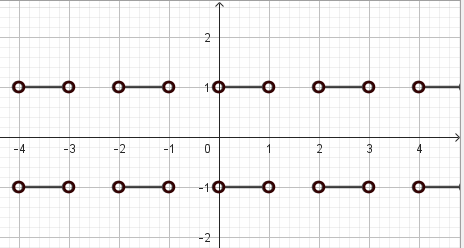
Zad. 3. Zaznacz na płaszczyźnie zbiór punktów o współrzędnych (x, y) spełniających równanie: [tex] |y|=\frac{|\sin\pi{x}|}{\sin\pi{x}} [/tex].
W maju punkty zdobyli:
- 3 – Artur Bumażnik ZS Elektronicznych Jelenia Góra, Zuzanna Czapiewska ZSB Słupsk, Aleksander Kiszkowiak I Technikum Elektroniczne Warszawa, Joanna Nowakowska LO Aslan Głogów, Cezary Rębiś ZS Elektronicznych Radom, Anastasia Yakovleva ZS Mogilno, Miłosz Zakrzewski LO Tuchola;
- 2,5 – Emilia Cichowska II LO Lubin, Julia ŚnieżekI LO Nysa, Michał Węgrzyn ALO PWr Wrocław;
- 2 – Radosław Górzyński I LO Lubin;
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad.1. Niech ABCD jest równoległobokiem, w którym |AB|=a, |BC|=b, |AC|= d1, |BD|= d2, a kąt BAD ma miarę 60º. Ponieważ d12 = a2+b2+ab i d22 = a2+b2–ab (dlaczego?), zachodzi [tex] \frac{a^2+b^2+ab}{ a^2+b^2-ab=\frac{19}{7} [/tex], skąd 6a2–13ab+6b2 = 0. Zatem [tex] 6(\frac{a}{b})^2-13\frac{a}{b}+6=0 [/tex], skąd [tex] \frac{a}{b}={3}{2} [/tex] lub [tex] \frac{a}{b}={2}{3} [/tex].
Zad. 2. Liczby spełniające warunki zadania spełniają układ równań xy = x+y i x+y = x2–y2. Z drugiego równania otrzymujemy x=-y lub y=x-1, a stąd rozwiązania (x, y) tego układu są następujące: (0, 0) lub [tex] (\frac{3-\sqrt{5}}{2}, \frac{1-\sqrt{5}}{2}) [/tex] lub [tex](\frac{3+\sqrt{5}}{2}, \frac{1+\sqrt{5}}{2}) [/tex].
Zad. 3. Funkcja f(x) = sinπx jest okresowa o okresie t=2. Jeżeli sinπx ≤ 0, to takie pary nie istnieją. Niech sinπx > 0. Wtedy |y|=1. Ale sinπx > 0 ↔ x∈ … ∪(-4, 3)∪(-2, -1)∪(0, 1)∪(2, 3)∪ …