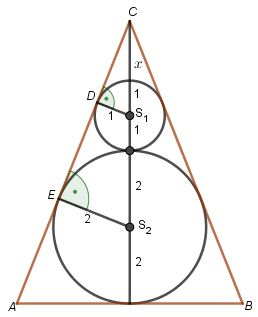
Zad. 1. Okrąg wpisany w trójkąt równoramienny ma promień równy 2, a okrąg styczny do dwóch ramion tego trójkąta i do okręgu wpisanego w ten trójkąt ma promień równy 1. Oblicz pole tego trójkąta.
Zad. 2. Podróżny przeszedł drogę z miasta A do miasta B i z powrotem w czasie 3 h 41 min. Droga z A do B biegnie najpierw do góry, potem po równinie, a pod koniec z góry na dół. Oblicz długość drogi biegnącej po równinie, jeżeli prędkość piechura pod górę wynosi 4 km/h, po równinie 5 km/h, a z góry na dół 6 km/h. Odległość z miasta A do B wynosi 9 km.
Zad. 3. Udowodnij, że nie istnieje trójkąt o bokach długości 20062016, 20072017, 20082018.
W maju punkty zdobyli
- 3 pkt. – Laura Stefanowska G Legnica, Piotr Zug SP 1 Borki Wielkie. Kacper Woszczek SP Mieroszów, Wojciech Szwarczyński SP Kowalowa, Maciej Michoń MZS Strzyżów, Oliwer Rum G 1 Głogówek, Agata Lefler ZSS Wołów, Tomasz Lefler ZSS Wołów i Marta Sibielec G 48 Wrocław;
- 2 pkt. – Gabriela Pietras SP Leszczyna;
- 1,5 pkt. – Maksymilian Szczepaniak SP Siechnice
- 1 pkt. – Joanna Galik SP 5 Wrocław, Hubert Bączyk G1 Swarzędz, Bartosz Nodzak SP 152 Łódź, Patrycja Zakrzewska G Tuchola.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech h oznacza wysokość trójkąta i h = 6 + x. Trójkąty prostokątne ES2C i DS1C są podobne (z cechy kąt-kąt), więc mają proporcjonalne boki i zachodzi 2/4+x = 1/1+x. Stąd x = 2, czyli h = 8. Stosując twierdzenie Pitagorasa do trójkąta DS1C, obliczamy |DC| = 2√2. Trójkąty prostokątne DS1C i AFC też są podobne (z cechy kąt-kąt), więc zachodzi |DC|:|DS1| = |CF|:|AF|, skąd |AF| = 2√2, czyli |AB| = 4√2. Pole trójkąta ABC wynosi więc 1/2·8·4√2 = 16√2.
Zad. 2. Oznaczmy przez x – długość drogi pod górę, y – długość drogi z góry, a – długość drogi po równinie. W drodze powrotnej część drogi, która biegła pod górę, jest z góry i na odwrót. Długość drogi z A do B wynosi x+a+y = 9. Czas trwania wędrówki w obie strony wynosi 3 h 41 min = 221/60 godz i na podstawie warunków zadania mamy x/4 + a/5 + y/6 + y/4 + a/5 + x/6 = 221/60. Rozwiązując układ równań, otrzymujemy po uproszczeniu x + y = 9 – a oraz 24a + 25(x+y) = 221, skąd a = 4. Długość drogi po równinie wynosi 4 km.
Zad. 3. Jeśli a, b, c oznaczają długości boków trójkąta, to z nierówności trójkąta zachodzi:
a+b > c, a+c > b i b+c > a.
Przyjmując a = 20062016, b = 20072017, c = 20082018, otrzymujemy natomiast a+b < c,
bowiem 20062016 + 20072017 < 2 . 20072017 < 2007 . 20072017 = 20072018 < 20082018.
Stąd wynika, że trójkąt o podanych długościach boków nie istnieje.
