Zad. 1. Pięciokąt ABCDE wpisano w okrąg. Wiedząc, że suma miar kątów przy wierzchołkach B i E jest równa sumie miar kątów przy wierzchołkach C i D wykaż, że |∡CAD| < 60° < |∡A|.
Zad. 2. W okręgu poprowadzono przecinające się cięciwy AB i CD. Na odcinku AB obrano punkt M tak, że |AM| = |AC|, a na odcinku CD obrano punkt N tak, że |DN| = |DB|. Wykaż, że jeśli M i N nie pokrywają się, to prosta MN jest równoległa do AD.
Zad. 3. Czworokąt ABCD wpisano w okrąg. Niech O1, O2, O3, O4 będą środkami okręgów wpisanych odpowiednio w trójkąty ABC, BCD, CDA i DAB. Wykaż, że czworokąt O1O2O3O4 jest prostokątem.
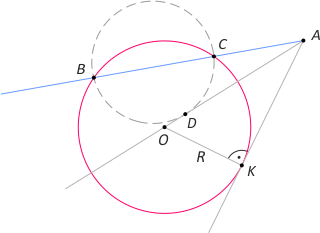
Zad. 4. (wolna amerykanka) Z punktu A leżącego na zewnątrz okręgu o środku O i promieniu R poprowadzono sieczną ACB (punkt C leży między A i B). Okrąg zbudowany na odcinku BC jako na średnicy jest styczny do odcinka AO w punkcie D. Oblicz długość AD, wiedząc, że długość AO wynosi a.
Za zadania 1-3 punkty otrzymali: 30 - Michel Migas (student PW), Dominik Bysiewicz (I LO Krosno), Krzysztof Lis (XIV LO Warszawa),Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Jacek Bagiński (nauczyciel matematyki, I LO Kraków) oraz Jerzy Kawka (I LO Kraków).
Za zadanie 4 punkty otrzymali: 10 - Jacek Bagiński, Dominik Bysiewicz, Krzysztof Lis, Michel Migas, Tadeusz Porzucek oraz Zygmunt Krawczyk (nauczyciel, SLO Żary).
Gratulacje!
Zad. 1. Z założenia |∡B| + |∡E| = t+x+φ+z+y+φ = x+t+z+t+z+y = |∡C| + |∡D|, a stąd 2φ = t+z. Dalej 360° = x+2y+2t+2z+2φ = 6φ+2x+2y, a stąd φ<60°. Z drugiej strony x+y = 180°–3φ > 0°. Ostatecznie |∡A| = x+φ+y > 60°.
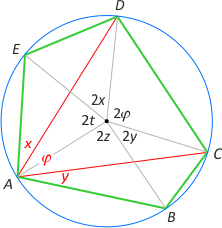
Zad. 2. Zauważmy, że trójkąty ACM i BND są równoramienne i mają równe kąty przy wierzchołkach A i D. Stąd mamy równość miar kątów zewnętrznych |∡CMB| = |∡CNB| = φ. Wynika z tego, że na czworokącie CBNM można opisać okrąg. Zatem |∡MNC| = |∡MBC|, bo są to kąty wpisane oparte na tym samym łuku MC. Z drugiej strony zachodzi |∡ABC| = |∡ADC|, bo są to kąty wpisane oparte na łuku AC. Otrzymaliśmy równość miar kątów odpowiadających, a stąd wynika teza.

Zad. 3. Łatwo zauważyć, że |∡AO1B| = 90° + |∡ACB|/2 oraz |∡AO4B| = 90° + |∡ADB|/2 (kąty między dwusiecznymi przy środku okręgu wpisanego w trójkąt). Ponadto |∡ADB| = |∡ACB|, bo są to kąty wpisane oparte na tym samym łuku AB. Stąd otrzymujemy |∡AO1B| = |∡AO4B|, która oznacza, że punkty A, B, O1 i O4 leżą na jednym okręgu. Zatem |∡AO1K| = α/2 i analogicznie |∡KO1O2| = γ/2. Zauważmy, że α+γ = 180°, a stąd |∡O4O1O2| = 90°. Miary pozostałych kątów wyliczamy analogicznie.

Zad. 4. Z punktu A prowadzimy styczną w punkcie K do okręgu o środku O. Z twierdzenia o siecznej i stycznej mamy |AD|2 = |AC|·|AB| oraz |AK|2 = |AC|·|AB|, zatem |AD| = |AK| = √(a2 – R2).




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
