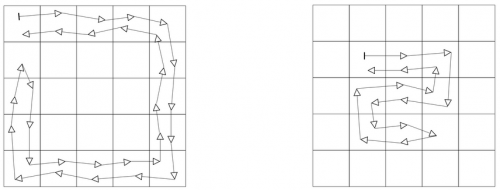
Zad. 1. Ania i Bartek grają w grę, która polega na skakaniu po kwadratowej szachownicy. Bartek skacze tylko po zewnętrznych polach, a Ania po wszystkich wewnętrznych (jak na rysunku dla szachownicy 5 na 5). Celem gry jest przeskoczenie po wszystkich swoich polach i powrót tą samą trasą na pole startowe. Skok zajmuje 1 sekundę. Ile czasu potrzebuje każde z nich na przeskoczenie swojej trasy na szachownicy 100 na 100?
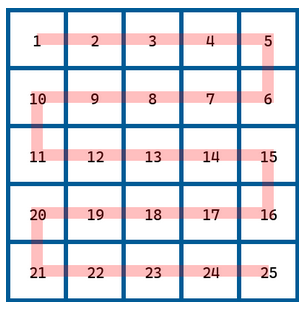
Zad. 2. Pola szachownicy 100 × 100 numerujemy "wężykiem" (jak na rysunku dla szachownicy 5 × 5). W której kolumnie i w którym wierszu znajdują się pola o numerach: 666, 1000, 2024?
Zad. 3. Zapisz algorytm, który pozwala odpowiedzić na pytanie z poprzedniego zadania dla dowolnego n ze zbioru {1, 2, 3, ..., 10000}.
W tym miesiącu po 3 punkty zdobyli: Krystyna Lisiowska - redaktor z Warszawy, Marcin Lorenz - manager IT z Mikołowa, Oliwia Makuch - studentka matematyki na PWr, Szymon Meyer - analityk danych z Dziewkowic, Kasper Przenzak - analityk ryzyka z Krakowa, Marzena Wąsiewicz - nauczycielka z Kajetan.
Gratulujemy!
Zad. 1. Bartek potrzebuje 720 sekund = 13 minut 10 sekund, a Ania - 19206 sekund = 5 godzin 20 minut 6 sekund.
Zad. 2. Położenie pół o numerach:
- 666 - wiersz 7, kolumna 66,
- 1000 - wiersz 10, kolumna 1,
- 2024 - wiersz 21, kolumna 24.
Zad. 3. Przykładowe rozwiązania:
a) wiersz := floor((n-1)/100)+1
kol := ((n-1) mod 100)+1
if ((wiersz mod 2)=0) kol := 101-kol
b) kol := ((n-1) mod 100)+1
wiersz := (n-kol)/100+1
if ((wiersz mod 2)=0) kol := 101-kol
c) wiersz := floor((n-1)/100)+1
if ((wiersz mod 2)=1) then
kol := (n-(wiersz-1)·100)
else
kol := 101-(n-(wiersz-1)·100)
d) wiersz := 1
kol := 1
kier := 1
dla i = 1 do n
if (i = n) zwróć (wiersz, kol)
else
kol := kol + kier
if (kol = 0)
kol := 1
wiersz := wiersz + 1
kier := 1
else if (kol = 101)
kol := 100
wiersz := wiersz + 1
kier := -1
