Zad. 1. W czworokącie wypukłym sumy długości przeciwległych boków są równe. Wykaż, że można w niego wpisać okrąg.
Zad. 2. Okrąg wpisany w trójkąt dzieli jedną ze środkowych na trzy równe odcinki. Znajdź stosunek długości boków tego trójkąta.
Zad. 3. W trójkącie równoramiennym ABC (gdzie |AB|=|BC|) dwusieczna BD jest dwa razy krótsza od dwusiecznej AE. Znajdź miary kątów tego trójkąta.
Zad. 4. (wolna amerykanka) Na trójkącie ABC opisano okrąg o środku O. Styczna do okręgu w punkcie C przecina prostą dzielącą kąt ABC na pół, w punkcie K, przy czym miara kąta CKB jest równa połowie różnicy miar potrojonego kąta CAB i kąta BCA. Suma długości boków AC i AB wynosi 2+√3, a suma odległości środka O od boków AC i AB wynosi 2. Znajdź promień okręgu opisanego.
Zadania kwietniowe okazały się trudne. Oto wyniki za zadania 1-3:
- 30 pkt. - Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) i Jacek Bagiński (nauczyciel matematyki, I LO Kraków),
- 20 pkt. - Dominik Bysiewicz (student UJ),
- 10 pkt. - Michał Malik (uczeń, I LO Kraków).
Za zadanie 4 punkty zdobyli:
- 10 pkt. - Tadeusz Porzucek,
- 8 pkt. - Jacek Bagiński,
- 2 pkt. - Michał Malik.
Gratulacje!
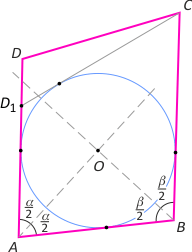
Zad. 1. Niech O będzie punktem wspólnym dwusiecznych kątów A i B. Oznacza to, że O jest środkiem okręgu stycznego do boków AB, BC i AD. Załóżmy nie wprost, że okrąg nie jest styczny do boku CD. Poprowadźmy przez wierzchołek C styczną do okręgu przecinającą prostą AD w punkcie D1. Wówczas czworokąt ABCD1 jest opisany na okręgu i mamy |AB|+|CD1| = |BC|+|D1A|. Z założenia zachodzi |AB|+|CD| = |BC|+|DA|. Odejmując te równości stronami, otrzymujemy ||CD1|–|CD|| = ||D1A|–|DA|| = |DD1|. Otrzymaliśmy sprzeczność polegającą na tym, że jeden bok trójkąta CDD1 jest równy różnicy pozostałych boków. Stąd wynika teza.
Zad. 2. Z twierdzenia o stycznej i siecznej (potęga punktu względem okręgu) mamy |AP|2 = |AR|2 = |AE|·|AF|, a stąd |AP| = |AR| = x√2. Analogicznie |M1Q| = x√2. Mamy zatem |AC| = |AP|+|PC| = |AP|+|CQ| = x√2 + |BC|/2 – x√2 = |BC|/2 oraz |AB| = |AR|+|RB| = |AR|+|BQ| = 2x√2 + |BC|/2. Stosując wzór na długość środkowej trójkąta (jego dowód wykorzystuje tylko twierdzenie Pitagorasa), mamy |AM1| = 1/2·√(2|AC|2+2|AB|2–|BC|2), skąd po podstawieniach i przekształceniach otrzymujemy |BC| = 5x√2/2 = 10x√2/4. Zatem |AB| = 13x√2/4 i |AC| = 5x√2/4. Stąd mamy szukany stosunek długości boków 5:10:13.

Zad. 3. Zauważmy, że BD jest jednocześnie wysokością i środkową boku AC. Przedłużmy BD tak, aby powstał romb ABCF. Wówczas trapez ABEF jest równoramienny, bo jego przekątne są równe. W rombie ABCF kąt CAF ma miarę 2α, a w trapezie ABFE kąt AFB ma miarę 3α. Rozważając trójkąt ADF, otrzymujemy α = 18°. Ostatecznie szukane kąty w trójkącie ABC mają miary 36°, 36° i 108°.

Zad. 4. (wolna amerykanka) Niech P i Q oznaczają odpowiednio środki boków AC i AB. Kąt KCA jest dopisany do okręgu i przystaje do kąta B, który jest wpisany i oparty na tym samym łuku.
A) Załóżmy, że punkt K leży na dwusiecznej kąta B (rys.1). Wówczas φ + β = α + β/2 (patrz na trójkąty KLC i ALB), skąd otrzymujemy γ = 90°. Oznacza to, że AB jest średnicą okręgu i |OP|=2, skąd |BC|=4 > 2+√3 = |AB|+|AC|, co daje sprzeczność. Należy zatem rozważyć inne położenie punktu K.
B) Załóżmy, że punkt K nie leży na dwusiecznej kąta B (rys.2). Tym razem mamy β/2 = α + φ, skąd otrzymujemy α = 30°. Zauważmy, że szukany promień równy jest bokowi BC, o długości a. Wystarczy więc obliczyć a.

Rozważymy przypadki ze względu na wielkość kąta B.
i) β<90° (rys. 3)
Uwzględniając, że |PQ| = a/2 (linia środkowa w trójkącie ABC) i stosując twierdzenie kosinusów w trójkącie OPQ, otrzymujemy a2/4 = |OP|2+|OQ|2–2|OP|·|OQ|·cos150°, skąd po podstawieniu |OQ| = 2–|OP| otrzymujemy równanie a2/4 = (2–√3)|OP|2 – 2(2–√3)|OP| + 4. Najmniejsza wartość trójmianu po prawej stronie równania wynosi 2+√3. Oznacza to, że a2 ≥ 4(2+√3) > (2+√3)2 i dalej a > 2+√3, co jest sprzeczne z nierównością trójkąta dla ABC.
ii) β = 90° (rys. 4)
Ten przypadek oznacza, że AC jest średnicą i |OQ| = 2, a stąd |BC| = 4 > 2+√3, co także daje sprzeczność.
iii) β > 90° (rys. 5)
Oznaczmy |OP|=x i |AT|=y. Wówczas |OT| = 2x√3/3, |TP| = x√3/3, |TQ| = y/2 oraz |AQ| = y√3/2. Korzystając z założeń, otrzymujemy układ równań |AP|+|AQ| = (2+√3)/2 oraz |OP|+|OQ| = 2. Po podstawieniu mamy równoważnie y + x√3/3 + y√3/2 = (2+√3)/2 oraz x + 2x√3/3 + y/2 = 2. Stąd x = 3/4, a y = (5–2√3)/2. Rozważmy teraz trójkąt OQP, w którym |OP| = 3/4, |OQ| = |OT|+|TQ| = 5/4. Z twierdzenia kosinusów otrzymujemy |QP| = √(34–15√3)/4, a stąd R = a = 2|PQ| = √(34–15√3)/2.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
