Zad. 1. Zapisano wszystkie liczby naturalne od 1 do 5555. Ile razy użyto cyfry 9?
Zad. 2. Suma kwadratów trzech kolejnych liczb nieparzystych dodatnich jest liczbą czterocyfrową o jednakowych cyfrach. Wyznacz takie trójki liczb nieparzystych.
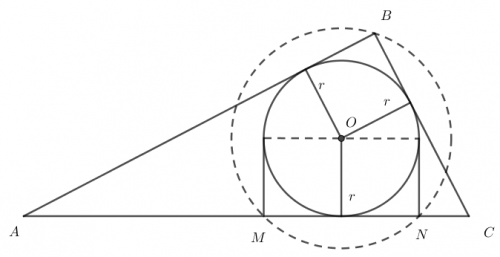
Zad. 3. W trójkąt prostokątny ABC wpisano okrąg. Rzut prostokątny tego okręgu na przeciwprostokątną AC jest odcinkiem MN. Oblicz miarę kąta MBN.
W grudniu punkty zdobyli:
- 3 – Artur Bumażnik ZSE Jelenia Góra, Emilia Cichowska II LO Lubin, Urszula Derkacz XL Warszawa, Aleksander Kiszkowiak I TE Warszawa, Karolina Szymandera I LO Inowrocław, Michał Węgrzyn ALO PWr Wrocław,
- 2 – Ewa Kucharska I LO Leszno, Julia Śnieżek I LO Nysa, Miłosz Zakrzewski LO Tuchola.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Wśród liczb od 1 do 10 na miejscu jedności jest jedna dziewiątka, podobnie wśród liczb od 11 do 20 itd. Na miejscu jedności jest w sumie 5550:10 = 555 dziewiątek. Na miejscu dziesiątek znajduje się 5500:10 = 550 dziewiątek (dlaczego?), a na miejscu setek 5000:10 = 500 (dlaczego?). Razem napiszemy 555+550+500 = 1605 dziewiątek.
Zad. 2. Niech n–2, n, n+2 będą trzema kolejnymi liczbami nieparzystymi i niech (n–2)2+n2+(n+2)2 będzie liczbą czterocyfrową o jednakowych cyfrach. Mamy wtedy 3n2+8 = 1111.k, gdzie k jest pewną cyfrą. Może zajść tylko k = 1, 5, 7. Dla k=1 i k=7 liczba 1111k–8 nie jest podzielna przez 3, co przeczy równości 3n2+8 = 1111.k. Dla k=5 znajdujemy n=43. Jedynym rozwiązaniem zadania jest trójka (41, 43, 45).
Zad. 3. Niech r oznacza długość promienia okręgu wpisanego w trójkąt ABC. Wtedy |OB| = |ON| = |OM| = r√2. Punkty M, N i B należą więc do okręgu o środku O i promieniu r√2. Kąt MBN jest wpisany w ten okrąg i opiera się na tym samym łuku, co kat środkowy MON, który jest prosty, zatem kąt MBN ma miarę 45°.
