Zad. 1. W trójkącie ABC środkowe AD i BE są wzajemnie prostopadłe a |AB|=2. Oblicz sumę kwadratów długości boków tego trójkąta.
Zad. 2. W trójkącie ABC zachodzi |AC|=16 i |BC|=10. Prosta przechodząca przez środek okręgu wpisanego w trójkąt dzieli bok AC na połowy, a bok BC na odcinki o długościach 3 i 7. Oblicz długość AB.
Zad. 3. Niech K będzie środkiem boku AB kwadratu ABCD. Przedłużmy KD do punktu O tak, by |∡KCO|=90°. Wiedząc, że pole kwadratu wynosi 36, oblicz pole trójkąta KCO.
Zad. 4. (wolna amerykanka) W trójkąt ABC, w którym cosB = 0,8 wpisano okrąg o promieniu 1, który jest styczny do linii średniej trójkata równoległej do boku AC. Oblicz długość boku AC.
Za zadania 1-3 punkty otrzymali:
-
30 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Dominik Bysiewicz (student matematyki na UJ), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Sławomir Matysiak (nauczyciel, X LO Wrocław), Mikołaj Popek (student UAM) oraz Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 20 - Janusz Wieczorek (emerytowany nauczyciel, Sandomierz) oraz Radosław Górzyński (uczeń, I LO Lubin).
Za zadanie 4 po 10 punktów otrzymali: Jacek Bagiński, Dominik Bysiewicz, Elżbieta Grzechnik, Mikołaj Popek, Tadeusz Porzucek, Janusz Wieczorek oraz Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy).
Gratulujemy!
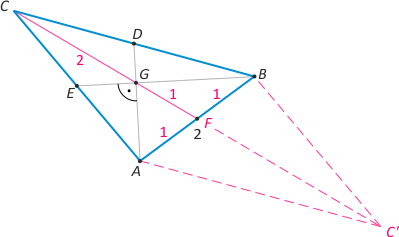
Zad. 1. Zauważmy, że środkowa GF trójkąta prostokątnego ABG (gdzie G jest środkiem ciężkości trójkąta ABC) jest dwa razy krótsza od przeciwprostokątnej AB (dlaczego?), więc ma długość 1. Stąd środkowa CF trójkąta ABC ma długość 3. Przedłużamy CF tak, by otrzymać równoległobok AC'BC. Korzystamy z faktu, że suma kwadratów długości przekątnych równoległoboku jest równa sumie kwadratów długości wszystkich jego boków, otrzymując równość |AB|2+|C'C|2 = 2(|AC|2+|CB|2), a po podstawieniu danych 36+4 = 2(|AC|2+|C'C|2), skąd |AC|2+|C'C|2 = 20. Ostatecznie szukana suma wynosi 24.
Zad. 2. Zauważmy, że PABC : PCDE = (1/2(26+x)·r) : (8r/2+7r/2) = (26+x)/15 (ozn. *). Niech DF będzie linią średnią trójkąta ABC. Wówczas PCDF : PFDE = 5/2, a stąd PCDF = 5/7·PCDE. Łatwo zauważyć, że PCDF = 1/4·PABC, a stąd PABC = 20/7·PCDE. Po podstawieniu do (*) otrzymujemy (26+x)/15 = 20/7, skąd x = 118/7.

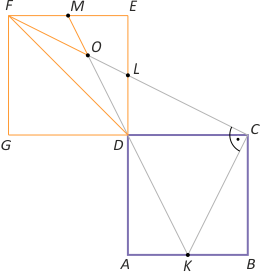
Zad. 3. Zbudujmy kwadrat DEFG, jak na rysunku. Niech L będzie punktem wspólnym odcinków CO i DE. Zauważmy, że trójkąty KCB i LDC są przystające z cechy kbk (oba są prostokątne, mają jednakowy bok i kąty DCL i KCB są przystające). Oznacza to, że L jest środkiem boku DE. Przedłużmy odcinek KD do przecięcia z FE w punkcie M. Otrzymujemy trójkąty przystające DEM i DAK, skąd wynika, że M jest środkiem boku FE. Oznacza to, że punkt O jest środkiem ciężkości trójkąta DEF. Ostatecznie PKCO = PODL+PDCL+PDKC = 1/6PFDE+1/4PABCD+1/2PABCD = 18/6+36/4+36/2 = 30.
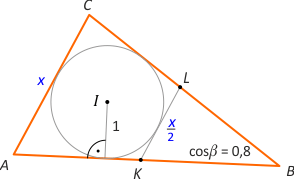
Zad. 4. Z "jedynki trygonometrycznej" mamy sinβ = 0,6. Rozważmy czworokąt AKLC. Wpisano w niego okrąg, więc |AC|+|KL| = |AK|+|LC| = 1/2(|AB|+|BC|), skąd |AB|+|BC| = 3x. Obwód trójkąta ABC wynosi zatem o = 4x, a jego pole o/2·r = 2x. Z drugiej strony PABC = 1/2|AB|·|BC|·sinβ = |AB|·|BC|·0,3. Iloczyn |AB|·|BC| obliczymy z twierdzenia kosinusów w trójkącie ABC, tzn. x2 = |AB|2+|BC|2–2·|AB|·|BC|·0,8 = (|AB|+|BC|)2–2·|AB|·|BC|–1,6·|AB|·|BC| = 9x2–3,6·|AB|·|BC|. Stąd |AB|·|BC| = 20x2/9. Zatem PABC = (20x2/9)·0,3 = 2x2/3. Porównując oba otrzymane wyniki, dostajemy równanie 2x2/3 = 2x, skąd x = 3.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
