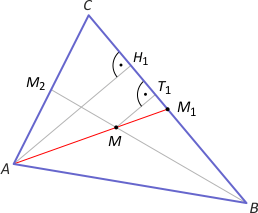
Zad. 1. Wewnątrz trójkąta ABC obrano punkt M taki, że pola trójkątów AMC, BMC i AMB są równe. Wykaż, że punkty A, M i środek boku BC leżą na jednej prostej.
Zad. 2. Dany jest tójkąt nierównoramienny ABC. Niech M oznacza jego środek ciężkości, a I - środek okręgu wpisanego (tzw. in-centrum). Wykaż, że jeśli odcinek MI jest prostopadły do prostej BC, to 3|BC| = |AC|+|AB|.
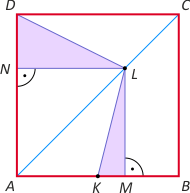
Zad. 3. Niech K będzie środkiem boku AB w kwadracie ABCD, a punkt L niech dzieli przekątną AC w stosunku |AL|:|LC| = 3:1. Wykaż, że kąt KLD jest prosty.
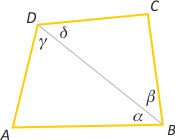
Zad. 4. (wolna amerykanka) Wskaż wszystkie czworokąty, w których sumy sinusów przeciwległych kątów są równe.
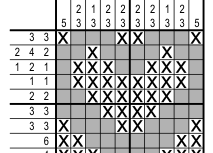
Punkty za zadania 1-3 otrzymali:
- 30 - Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) ,
- 20 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Michał Malik (uczeń, I LO Kraków), Mikołaj Popek (VIII LO Poznań), Szymon Wróblewski (SP 5 Opole),
- 10 - Filip Derejski (I LO Kraków).
Za zad. 4 (wolna amerykanka) 10 pkt. otrzymali: Tadeusz Porzucek, Jacek Bagiński i Adrian Michałowicz (matematyk z Poznania). Gratulacje!
Przy okazji osobne gratulacje należą się uczestnikowi naszej Ligi - Dominikowi Bysiewiczowi (studentowi UJ), który w czerwcu zajął II miejsce w tegorocznych Mistrzostwach Polski w Geometrii Elementarnej. Brawo!
Zad. 1. Niech M1 i M2 oznaczają przecięcie prostych AM i BM z bokami odpowiednio BC i AC. Z założenia PAMB = PBMC = PAMC = 1/3 PABC. Rozważmy trójkąty ABC i BMC. Zachodzi 1/3 = |MT1|:|AH1|, gdzie MT1 i AH1 są wysokościami tych trójkątów. Z drugiej strony z twierdzenia Talesa mamy |MM1|:|AM1| = 1/3, a stąd |AM|:|MM1| = 2. Analogicznie |BM|:|MM2| = 2. Oznacza to, że AM1 i BM2 są środkowymi, a punkt M jest środkiem ciężkości trójkąta ABC. Stąd wynika teza.
Zad. 2. Opiszmy okrąg na trójkącie ABC i niech W1 oznacza punkt przecięcia dwusiecznej AI z tym okręgiem. Zauważmy, że trójkąty ABW1 i AL1C są podobne z cechy kkk (bo mają kąty równe α/2 i kąty oparte na łuku AB). Wobec tego mamy |BW1|:|AW1| = |CL1|:|AC|. Z zasady trójliścia (patrz rozwiązanie zadania 3 z Lutego 2014) mamy |BW1| = |IW1|, a stąd mamy też |IW1|:|AW1| = |CL1|:b. Z równoległości MI i M1W1 mamy |IW1|:|AW1| = |M1M|:|AM1| = 1/3. Łatwo stąd otrzymać, że |CL1| = b/3. Analogicznie dowodzimy, że |BL1| = c/3. Stąd wynika teza.

Zad. 3. Niech M i N będą rzutami prostokątnymi punktu L odpowiednio na boki AB i AD. Z twierdzenia Talesa mamy |MB|:|AM| = |LC|:|AL| = 1/3, a stąd mamy |MB| = |AM|/3 = |AB|/4. Dalej |KM| = |AM|–|AK| = 3/4|AB| – 1/2|AB| = |AB|/4. Oznacza to, że |KM|=|MB|=|ND|. Wobec równości |LM|=|LN| łatwo zauważyć przystawanie prostokątnych trójkątów KML i LND (jednakowe przyprostokątne). Zatem kąty MLK i NLD są przystające. Mamy zatem |∡KLD| = |∡KLN| + |∡NLD| = |∡KLN| + |∡MLK | = |∡NLM| = 90°.
Zad. 4. Przy przyjętych założeniach mamy sinA = sin(180°–(α+γ)) = sin(α+γ)
oraz sinC = sin(β+δ). Dalej z założenia mamy sin(α+γ) + sin(β+δ) = sin(α+β) + sin(γ+δ). Stosując wzór na sumę sinusów, otrzymujemy 2sin((α+β + γ+δ)/2)· cos((α+β–γ–δ)/2) = 2sin((α+β+γ+δ)/2)· cos((α+γ–β–δ)/2), a po skróceniu cos((α+β–γ–δ)/2) = cos((α+γ–β–δ)/2). Stosując wzór na różnicę kosinusów, mamy -2sin(α–δ)sin(β–γ) = 0. Zatem α–β = 0 lub β–γ = 0, a stąd α=δ lub β=γ, co oznacza, że przynajmniej jedna para boków czworokąta jest równoległa. Szukanymi czworokątami są zatem trapezy lub równoległoboki.